Мир приключений, 1928 № 07 ,

Редактирует ЗАГАДАЙ-КА

КОНКУРС НА ПРЕМИИ № 6 откладывается до будущего номера, т. к читатели имеют сейчас в проработке задачи по конкурсам № 3 и № 5.

РЕШЕНИЯ ЗАДАЧ НА КОНКУРСЕ № 2.

Кратчайший путь.

Задача № 4.

Задача не исчерпана по всем предложенным в ней вопросам. Даем решение лишь частично, в уверенности, что читатели не упустят сами довести решение до конца.

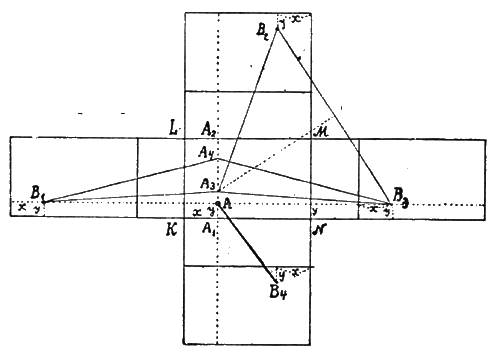
Для нахождения искомого пути надо развернуть все стены, потолок и пол комнаты в одной плоскости, напр., в плоскости пола. Затем в последней плоскости надо соединить обе данные точки прямой линией. И так как разверток может быть несколько, то из всех проведенных прямых надо выбрать наименьшую. На схеме показаны 4 возможных развертки, которые разнятся в положениях потолка (может ли быть разверток свыше четырех?) Для требуемого соединения точки А на полу с точкой В на потолке кратчайший путь будет (см. графику) АВ4. — Является-ли такой путь всегда единственно возможным? И когда равных путей будет несколько?

Это обнаружится яснее, если точку на потолке держать неизменно на одном и том же месте, а для точки на полу искать различные места. Пусть, напр., точки B₁, В₂, В₃и В₄, обозначающие одну и ту же точку В в различных развертках, везде одинаково отстоят от ближайших ребер потолочной грани — в расстояниях х и у (см. графику). Тогда Прямая А₁А₂, проведенная по полу параллельно стороне KL в удалении от нее на величину х, будет геометрическим местом точек, равно отстоящих от В₁ и В₃. Другими словами, для каждой точки, лежащей на прямой А₁А₂, будет два равных пути в потолочную точку: как через левую стену, так и через правую (напр, для точек А₃ и А₄: это потому, что АВ₁ = АВ₃). В частности же для точки на полу А₃ будет три одинаковых пути к потолочной точке, если А₃ будет лежать на пересечении с перпендикуляром, восстановленным к линии В₂ В₃ из ее середины (тогда A₃В₁ = А₃В₂ = А₃В₃; эти пути, не в пример приведенной графике, могут быть и кратчайшими).

Анализируя многие иные случаи, с учетом относительных размеров самой комнаты, можно определить все те частные условия, при которых число решений задачи будет доходить даже до шести.

_____ РЕШЕНИЯ ЗАДАЧ НА КОНКУРСЕ № 2.

Криптограмма.

Задача № 5.

«Своим светом освети чужую тьму и все тебе будет приятно».

(«Исповедь» М. Горького).

Из пятиугольника квадрат.

Задача № 6.

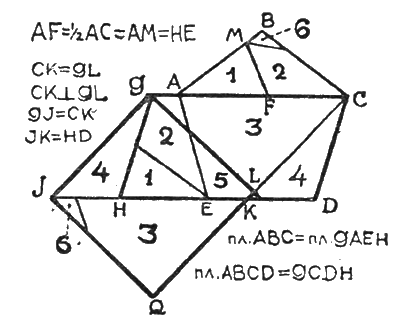
Из прямоуг. треугольника СОЕ гипотенуза СЕ будет равнятся ½ √5 (считая радиус СО=1, а ОЕ =½; см. рис. в. № 3 журнала). Значит FO = FE — OF = CE — ОЕ = ½ √5 — ½ = ½(√5–1). Последняя же формула является выражением стороны правильного десятиугольника, вписанного в окружность радиуса = 1. Следовательно в треугольнике COF катеты таковы: OF — сторона десятиугольника, а СО — радиус описанной окружности; в таком случае гипотенуза FC будет стороной правильного пятиугольника (в курсах геометрии есть такая теорема, то же ясно при определении длины СF = ½√(10 — 2 √5). Итак, фигура MCNLK, построенная на базе CF, есть правильный пятиугольник.

Вторая, более трудная часть задачи, решена в построении, приведенном рядом — ABCDE — данный пятиугольник. F — середина его диагонали АС. AM = AF и HE =AF, a GH параллельна CD. Нетрудно разобрать, что параллелограмм GCDH равновелик ABCDE, так как у этих двух фигур, при их общей части ACDE, дополнительные площади АВС и GAEH равны между собой. Значит, остается превратить параллелограмм GCDH в равновеликий ему квадрат; ясно, что сторона этого квадрата будет средней пропорциональной между основанием и высотой параллелограмма. Пусть GL = CK проведены под прямым углом одна к другой; тогда GL и будет стороной искомого квадрата (нетрудно доказать, что GL = CK есть средняя пропорциональная между основанием и высотой параллелограмма). Если теперь GI параллельна СК, a IQ параллельна GL, то легко убедиться, что GLQI и есть искомый квадрат (GI=CK, a IQ — GL). Помимо долей №№ 1, 2 и 5, входящих в параллелограм и уже отвечающих таким же долям в ABСDE, еще три доли 3, 4 и 6 тоже соответственны равны долям квадрата, обозначенным теми лее номерами.　

В результате искомый квадрат выкладывается по нашему чертежу при разрезании данного пятиугольника всего на шесть частей (в премированных решениях дается деление от 7 до 13 частей). Неправильными математически, хотя и близкими по размерам, являются те решения, где сторона искомого квадрата приравнивается полусумме из стороны пятиугольника и его диагонали. Предлагаем любителям подсчетов определить цифровую разницу в таком неправильном решении сравнительно с верным.　

_____ ИТОГИ КОНКУРСА НА ПРЕМИИ № 2

Вследствие происшедшего запоздания в выходе №№ 3 и 5, —запоздания, независящего ни от редакции, ни от издательства, — этот конкурс вышел неудачным, так как подписчики не имели достаточно времени для решения предложенных задач. В конкурсе приняло участие всего 15 человек, из коих по 3 задачам получили зачеты 8 человек, по 2 задачам — 4 чел. и по 1 задаче — 3 чел. Оценка очками: трое — по 11 очков (по жребию премии 1–3), трое — по 9 очков, двое — по 7 очков, двое — по бочков, а остальные — менее 5 очков.

ПРЕМИИ РАСПРЕДЕЛЕНЫ ТАК:

1-я премия. Издание «Красота форм в природе» — проф. Геккеля (атлас ценностью в 26 рублей) — Н. В. Успенский (Тула). — 2-я премия. «Демон» Лермонтова (худож. изд. ценностью в 8 руб.) — А. С. Базаров (Ленинград) — 3-я премия. «Наука о небе и земле». — Е. Игнатьева, (ценность изд. 5 р.) — С. И. Соколов (Москва). — 4-я премия. Сочинение проф. С. О. Грузенберга «Гений и творчество» — Б. В. Замбржицкий (Ленинград), — 5-я—10-я премии. Книги из числа указанных в условии конкурса: 5) В. А. Янковский (Ленинград); 6) Б. В. Смирнов (Одесса); 7) И. Б. Горцев (Ростов); 8) В. И. Лапин (Новгород); 9) X. Файфман (Киев); 10) И. Федоров (Минск).