Загадка падающей кошки и фундаментальная физика

Как мы уже знаем, Максвелл участвовал в не слишком строгих экспериментах с переворачиванием кошек еще в 1850-е гг., хотя никогда и не публиковал официально никаких гипотез или наблюдений на этот счет ни в каких научных журналах. Однако он, очевидно, часто обсуждал свои идеи с другом всей жизни и коллегой — тоже шотландским физиком Питером Гатри Тэйтом. Когда Максвелл неожиданно умер в 1879 г. в возрасте 48 лет, Тэйта попросили написать некролог на его смерть для престижного журнала Nature. Помимо упоминания о впечатляющих достижениях Максвелла в области электромагнетизма, термодинамики, астрономии, теории цвета и механики Тэйт счел нужным упомянуть и частные мысли Максвелла на тему переворачивания кошек:

В студенческие дни он провел один эксперимент, который, хотя и оказался в определенной степени физиологическим, был тесно связан с физикой. Его целью было определить, почему кошка всегда приземляется на лапы, как ее ни бросай. Аккуратно бросая кошку на расстеленный на полу матрас и придавая ей различное начальное вращение, он убедился, что кошка инстинктивно пользуется законом сохранения момента импульса: она вытягивает свое тело, если вращается слишком быстро и есть опасность упасть головой вниз, и собирается в клубок, если вращается слишком медленно^{8}.

Описание, данное Тэйтом, поясняет нам, как могло бы, в принципе, работать объяснение об обязательном отталкивании кошки от неподвижной опоры. Откуда кошка может знать, как сильно следует оттолкнуться, чтобы развернуться в точности на правильный угол? Ответ, согласно Максвеллу, состоит в том, что она этого не знает: кошка при помощи задних лап регулирует скорость вращения так, чтобы приземлиться на лапы. Это могло бы работать примерно так же, как фигурист регулирует скорость вращения на льду: подтягивает руки к телу, чтобы вращаться быстрее, и раскидывает их в стороны, чтобы замедлить вращение. Аналогично, рассуждал Максвелл, и кошка может регулировать скорость своего вращения, вытягивая или поджимая лапы и меняя тем самым момент инерции, чтобы управлять скоростью вращения.

Это объяснение тоже было неверным, как показали фотографии Марея. В защиту Максвелла заметим, что сам он никогда не публиковал эти свои идеи, из чего можно предположить, что он не считал их достаточно сильными, чтобы представлять широкой публике. Опубликованы они были только по инициативе Тэйта. Но совместной мощи ученых репутаций Максвелла и Делоне было достаточно, чтобы гипотеза «точки опоры» прочно угнездилась в умах членов Французской академии, что и привело в конечном итоге к спору на судьбоносном заседании в октябре 1894 г.

К счастью, после того как прошел первоначальный шок от лицезрения «научного парадокса» Марея, французские академики овладели собой. Взяв небольшой перерыв для размышлений о физике и математике, скромные члены Академии пришли на следующее собрание подготовленными.

На следующем собрании месье Морис Леви поднялся и сказал, что, по его мнению, вся сложность этого случая берет начало из неточной интерпретации некоторых фундаментальных принципов механики. После этого он прошел к доске и быстро покрыл ее значками, которые ясно доказали, до самого глубокого понимания, что кошка падением своим не нарушает никаких математических законов. Мир воцарился в Академии: Causa finita est («Дело завершено»)^{9}.

Леви точно описал источник заблуждения. Физики пали жертвой хрестоматийной проблемы, состоящей в том, что «полузнание хуже невежества». В данном случае все физики, о которых идет речь, рассматривали — как поступали и мы в данной главе — вращающиеся тела, которые были более или менее жесткими: руки можно развести или сложить, но изгибы и вращения самого тела во внимание не принимались. Их поверхностное представление о вращающихся телах и законе сохранения момента импульса было основано на рассмотрении именно таких жестких волчков. Кошек же ни в коем случае нельзя рассматривать как жесткие тела.

Новая гипотеза о переворачивании кошки, в то время удовлетворившая, очевидно, большинство членов Академии, была предложена французским математиком Эмилем Гийю, больше известным в качестве автора одного из типов картографической проекции Земли на плоскую карту, называемого сегодня проекцией Гийю^{10}. Чтобы разобраться в «кошачьей» гипотезе Гийю, вспомним для начала пример человека, вращающегося в офисном кресле. Примерно как фигуристка на льду, человек в кресле тоже может контролировать поворот кресла, разводя или сгибая руки при повороте верхней части корпуса. Если руки разведены, человек обладает высоким моментом инерции и кресло повернется в обратную сторону на значительный угол. Если руки сложены, то момент инерции у человека невысок и кресло повернется в обратном направлении на относительно небольшой угол. Регулируя личный момент инерции по отношению к моменту инерции кресла, человек может управлять тем, насколько сильно — или слабо — повернется в обратном направлении кресло.

Аналогично Гийю представил себе, что кошка могла бы при помощи своих передних и задних лап управлять моментом инерции передней и задней частей тела. В первоначальном падении, рассуждал Гийю, кошка должна была бы вытянуть задние лапы и подобрать под себя передние. Тогда она могла бы повернуть верхнюю часть тела так, чтобы правильно сориентировать ее относительно земли, не получив при этом существенного обратного поворота нижней части тела. Затем кошка подобрала бы под себя задние лапы, вытянула передние и провернула нижнюю часть тела до правильной ориентации, чтобы целиком принять правильное положение в пространстве, не получив при этом существенного обратного поворота верхней части тела.

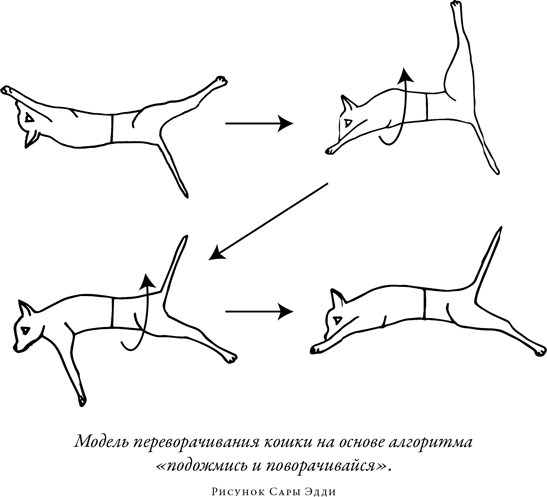
Марей поддержал это объяснение, и позже оно получило известность как модель переворачивания кошки типа «подожмись и поворачивайся». Качественное объяснение Гийю поддержал и Морис Леви, который при помощи строго математического анализа, основанного на теореме площадей, показал, что это объяснение по крайней мере правдоподобно с физической точки зрения. Даже Марсель Депре, один из самых яростных защитников Делоне, в конечном итоге принял новый взгляд на теорему площадей и, замечательно извернувшись, припомнил, что именно он побудил Марея сделать те самые фотографии падающей кошки.

Мне казалось, что способности, которыми пользуется животное для получения этого замечательного результата, с точки зрения приведенной выше теоремы [теоремы Делоне] обладают огромной важностью, но, не имея в своем распоряжении никакого устройства для мгновенной фотографии, я подумал, что лучше всего будет рассказать о своих идеях мистеру Марею, который имеет все средства исследования, которых у меня нет, и я несколько раз при случае выразил ему пожелание обратиться к этому вопросу возможностями мгновенной фотографии. Сегодня я доволен своей настойчивостью, потому что опыт, результаты которого он представил Академии, привлек, как я ему сказал, внимание к следствиям из теоремы площадей и высветил ту ошибку, жертвами которой стал не только Делоне, но и все авторы трактатов по теоретической механике^{11}.

Объяснения и Гийю, и Леви появились сразу же после публикации в журнале Comptes Rendus статьи Марея, посвященной его фотографиям; похоже, академики спешили оправдаться после тех насмешек со стороны СМИ, которым они подверглись. Даже научные публикации на эту тему часто не обходились без забавных деталей; так, в описание фотографий Марея в журнале Nature входила оценка позиции самой кошки: «Выражение оскорбленного достоинства, продемонстрированное кошкой в конце первой серии фотографий, указывает на недостаток интереса к научному исследованию с ее стороны»^{12}.

Из академической дискуссии, однако, было неясно, действительно ли алгоритм Гийю описывает способ, при помощи которого кошки переворачиваются на самом деле. Тем не менее это объяснение было принято как факт и через несколько лет попало даже в учебники по физике. Этот пример, в частности, содержится в книге по «динамике системы твердых тел» 1897 г. издания:

Пример 3. Объясните, как кошка, которую подняли лапами кверху и отпустили, оказывается, упав с достаточной высоты, в правильном положении и приземляется на лапы.

На первом этапе падения кошка вытягивает задние лапы почти перпендикулярно оси тела и подтягивает передние к шее. В этом положении она поворачивает переднюю часть тела на как можно больший угол; при этом задняя часть тела поворачивается на меньший угол в обратном направлении, так что полная сохраняющаяся площадь относительно этой оси равна нулю… На втором этапе падения положение лап меняется на обратное, задние поджимаются к телу, а передние вытягиваются. Теперь кошка поворачивает заднюю часть тела на больший угол, а переднюю в обратном направлении — на меньший. В результате обе части тела кошки оказываются повернутыми вокруг оси на почти одинаковые углы^{13}.

Хотя задача, кажется, была наконец решена, не следует переоценивать влияние, произведенное откровением падающей кошки на мышление физиков того времени. Марей при помощи всего лишь небольшого числа фотографий наглядно продемонстрировал две важные истины. Первая состоит в том, что, хотя законы физики, такие как закон сохранения момента импульса, невозможно нарушить, их можно «обойти» самыми неожиданными способами, которые делают возможными вещи, на первый взгляд кажущиеся невозможными. Вторая истина — то, что природа давно уже нашла многие пути «обхода» и что более тщательное исследование природы потенциально может оказаться полезным в решении задач, которые ставят ученых в тупик.

Статьи, посвященные задаче падающей кошки, продолжали выходить в Comptes Rendus на протяжении еще нескольких месяцев после публикации работы Марея; в них авторы продолжали разрабатывать поднятую тему. В одной из таких статей, написанной Леоном Лекорню в конце 1894 г., отмечается, что другие животные, в принципе, могут использовать для переворачивания другие стратегии:

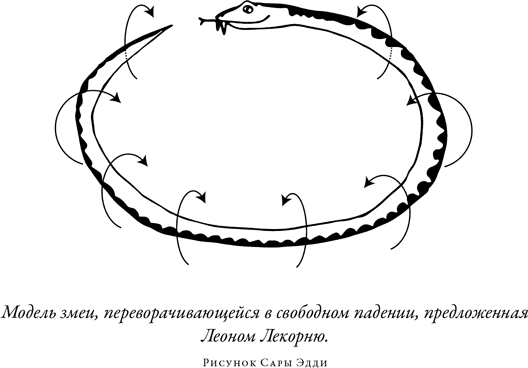
Еще более простой пример переворачивания за счет внутренних сил можно увидеть в движении змеи, если представить себе, что она изогнута на плоскости в форме тора и ее сечения вращаются, каждое в своей плоскости, с одинаковой угловой скоростью. Теорема площадей при этом, очевидно, будет соблюдаться, а внешняя форма змеи не только будет оставаться постоянной, но и покажется неподвижной в пространстве, несмотря на то что спинка змеи при этом окажется на месте ее живота и наоборот. Нет ничего невозможного в том, чтобы подобный процесс использовался некоторыми водными животными^{14}.

В сущности, Лекорню представил себе змею, сворачивающуюся в кольцо подобно бублику или уроборосу, а затем как бы проворачивающую себя вокруг центральной оси позвоночника. Момент импульса от вращения сегмента змеиного тела с одной стороны бублика уравновешивается моментом импульса от сегмента на другой его стороне, вращающегося в противоположном направлении.

Модель Лекорню не была воспринята как серьезное описание движения змеи, хотя мы увидим, что она, как ни смешно, ближе к кошачьему методу переворачивания, чем модель Гийю. Попутно отметим, что в Юго-Восточной Азии есть род змей Chrysopelea, представителей которого называют летающими змеями из-за их способности и склонности парить — слетать с древесных ветвей на землю. Эти змеи добиваются парения тем, что уплощают свое брюшко и изгибают тело волной. Зрелище летящей змеи стоит того, чтобы отыскать соответствующее видео.