Загадка падающей кошки и фундаментальная физика

А если вы махнете длинной палкой в горизонтальной плоскости, ваше тело повернется в противоположном направлении. Эта палка соответствует кошачьему хвосту.

Пеано дал простое и элегантное объяснение — даже слишком простое и элегантное: почти столетие спустя, в 1989 г., Дж. Э. Фредериксон экспериментально продемонстрировал, что бесхвостая кошка прекрасно умеет переворачиваться, хотя кошки, у которых хвосты имеются, действительно используют их, чтобы помочь процессу^{2}. Но объяснение с привлечением хвоста-пропеллера очень характерно для такого математика, как Пеано, для его стиля, эрудиции и интересов.

Джузеппе Пеано (1858–1932), видный математик-исследователь, опубликовал более 200 книг и статей. Он вырос на ферме в итальянской деревне Спинета и начальное образование получил в деревенской школе, где в холодные месяцы учащимся приходилось приносить из дома поленья, чтобы обогревать здание школы во время уроков^{3}. Учился Пеано отлично, и рано проявившиеся выдающиеся способности мальчика не остались незамеченными: около 1870 г. его дядя предложил ему пожить у него и поступить на учебу в Турине. Там Пеано посещал известную школу, а после ее окончания в 1876 г. поступил в Туринский университет, где ему суждено было провести всю свою трудовую жизнь. После окончания университета в 1880 г. он стал помощником Анджело Дженокки, заведующего кафедрой дифференциального и интегрального исчисления, и получил право как на преподавание, так и на собственные математические исследования.

Именно во время работы под руководством Дженокки мы видим в Пеано первые предвестники будущих конфликтов. Судя по всему, он жаждал сделать себе имя. В 1882 г., к примеру, он совершил свое первое значимое математическое открытие: обнаружил ошибку в важной формуле, опубликованной в получившем широкое распространение учебнике по математическому анализу. Пеано хотел исправить формулу, но узнал от Дженокки, что и ошибка, и правильный вариант были уже найдены два года назад, хотя и не опубликованы. За этим последовала переписка между Пеано, Дженокки и первооткрывателем Германом Шварцем, а также некоторыми другими математиками, которая продолжалась несколько лет без особого результата. В 1890 г., когда сообщение об ошибке было наконец выпущено, опубликовал его амбициозный Пеано, а не Шварц.

Еще один пример включает уже прямое столкновение между Дженокки и Пеано. Лекции Дженокки по дифференциальному и интегральному исчислению высоко ценились в университете, и в 1883 г. Пеано попытался уговорить старшего коллегу собрать их в книгу. Дженокки отказался, отговорившись плохим здоровьем, но Пеано сказал, что может сам написать книгу от имени Дженокки. Книга Анджело Дженокки под названием «Дифференциальное исчисление и начала интегрального исчисления» (Calcolo differenziale e principii di calcolo integrale) вышла в конце 1884 г. с примечанием: «С добавлениями д-ра Джузеппе Пеано».

Это издание породило, по крайней мере поначалу, небольшой скандал. Пеано не только собрал и скомпилировал лекции Дженокки, но и включил в книгу то, что сам он назвал «важными добавлениями». Эта формулировка производила впечатление одновременно эгоизма и неуважения к человеку, обозначенному в книге как автор. Как может молодой выскочка улучшить работу мастера? Сам Дженокки тоже сначала рассердился, хотя со временем он, кажется, в целом оценил книгу по достоинству. Задним числом можно сказать, что добавления были очень важными.

Несмотря на довольно нахальный подход Пеано к самопродвижению — или, скорее, отчасти благодаря ему — он стремительно двигался по карьерной лестнице и набрал влияние. В 1886 г. Пеано занял второй пост профессора в Королевской военной академии, а в 1890 г. получил пожизненный пост профессора в Турине. Именно в этот период он опубликовал свои самые интересные и важные работы. Одним из величайших его достижений было формулирование того, что мы сегодня называем аксиомами Пеано, — небольшого набора простых утверждений, описывающих все свойства натуральных чисел (0, 1, 2, 3, …). Он также был разработчиком и пропагандистом формального стандартизованного «языка», который можно использовать для формулирования математических утверждений. Этот язык позволяет резко сократить математические доказательства, которые зачастую бывают чрезмерно громоздкими. Нотация Пеано до сих пор используется в почти неизменном виде. В 1890 г. он стал одним из основателей журнала Rivista di Matematica, в котором опубликовал свою первую «кошачью» статью «Принцип площадей и история кошки», а в 1891 г. начал «Стандарты проектов» (Formulario Project), целью которой было создание стандартизованной энциклопедии математики с использованием разработанного им символьного языка.

Еще один образец работы Пеано стоит того, чтобы упомянуть его здесь: это концепция заполняющей пространство кривой. Идею такой кривой представим вопросом: можно ли нарисовать одну-единственную кривую, которая полностью заполняет квадрат? Если говорить о карандаше и бумаге, то мы всегда можем заполнить квадрат, поскольку кончик грифеля имеет конечную толщину. Однако в математике линия — это объект, имеющий длину, но не имеющий ширины, тогда как квадрат имеет и длину, и ширину. Интуитивно нам представляется, что в этом смысле квадрат «больше», чем линия. Мы часто характеризуем это, называя размерности объектов: линия — одномерный объект, а квадрат — двумерный.

К концу XIX в. развитие математики позволило продемонстрировать, что число идеальных точек в линии и квадрате совершенно одинаково. Это значит, в принципе, что квадрат можно заполнить одной непрерывной линией, и именно Пеано первым показал в явном виде, как это сделать. Конструкция, которую он использовал, показана на рисунке, где квадрат заполняется линией, описывающей все более извилистую траекторию. На первом шаге траектория имеет попросту S-образную форму. В следующей итерации на отдельных участках траектории делаются свои S-образные ответвления, в следующей — ответвления на участках ответвлений и т. д. Пеано сумел строго доказать, что, произведя такую операцию бесконечное число раз, мы получим единую неразрывную линию, проходящую через каждую точку квадрата — мало того, проходящую через каждую точку не по одному разу^{4}.

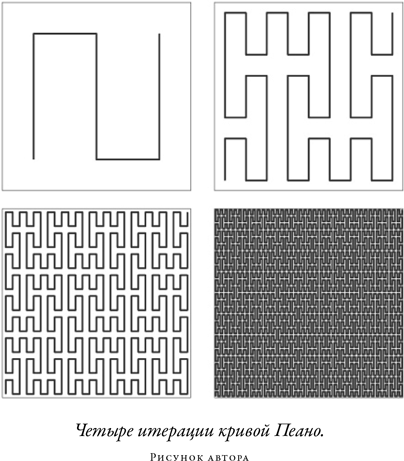
Много позже математики поймут, что Пеано открыл весьма любопытный образец интереснейшего математического объекта — фрактала. Обычные геометрические объекты имеют размерности, задаваемые не дробными числами, — квадрат двумерен, тогда как линия одномерна, — и у каждого объекта это число является, в определенном смысле, мерой того, сколько пространства занимает объект. Фракталы — объекты с дробной размерностью, и это указывает на то, что занимаемое фракталом количество пространства принципиально отличается от количества пространства, занимаемого простыми объектами. К примеру, фрактал с размерностью 1,5 занимает больше пространства, чем линия, но меньше, чем квадрат. Фракталы часто описывают как объекты, которые на любом уровне увеличения выглядят в основном одинаково — примерно как тонкий срез ветки дерева с виду похож на толстый срез ветки. Это самоподобие присутствует и в кривой Пеано. В общем, Пеано в своей необычной конструкции обнаружил необычный фрактал с фрактальной размерностью, равной 2, — не дробный фрактал.

Как мы уже видели, Пеано был амбициозным и изобретательным математиком, которого, как правило, интересовали крупные проекты. Однако он также всегда стремился показать, что серьезные математические инструменты, которыми он пользовался, применимы и к решению реальных практических задач. Обдумав на протяжении некоторого времени проблему падающей кошки, он увидел в ней объяснение одной из геофизических задач, вызывавших в то время большой интерес, — чандлеровского колебания полюсов.

Ко времени Пеано астрономы уже поняли, что направление оси вращения Земли не постоянно. Подобно оси вращающегося волчка или гироскопа, эта ось описывает своим концом окружность, что называется прецессией. Полный цикл прецессии земной оси составляет 26 000 лет. На пути своем ось слегка колеблется, или претерпевает нутацию, с периодом 18,6 года. Прецессия и нутация вызываются взаимодействием Земли с гравитационными силами Солнца и Луны.

Еще одну форму нутации предсказал в 1765 г. математик Леонард Эйлер. Он предположил, что сфероидальная (слегка несферическая) форма Земли допускает «свободную нутацию»: дополнительные небольшие колебания земной оси по отношению к твердой Земле, которая автономна и не подвержена действию внешних сил. Эти колебания возникают потому, что ось симметрии Земли слегка отличается от ее же оси вращения. После некоторой замечательной математической гимнастики Эйлер предсказал, что эта свободная нутация должна иметь период 306 суток.

Ожидалось, что такие колебания должны представлять собой чрезвычайно маленькие изменения в направлении земной оси; для их регистрации требовались тщательные измерения положения звезд в том виде, как они видны с Земли, на протяжении по крайней мере года. Такие серьезные препятствия ученые рассматривают как вызов для себя, и на протяжении более чем 100 лет многочисленные исследователи пытались наблюдать предсказанную Эйлером свободную нутацию. Никто из них не добился успеха, и к 1880-м гг. астрономы, в сущности, сдались и отказались от поисков этого эффекта.

Примерно в это же время Сет Карло Чандлер-мл. (1846–1913), эксперт по страхованию жизни и астроном-любитель, по счастливой случайности обнаружил то самое явление, которое успешно ускользало от внимания стольких профессионалов^{5}. Чандлер родился в Бостоне, штат Массачусетс, и впервые столкнулся с наукой во время обучения в последнем классе школы, когда получил работу у гарвардского математика Бенджамина Пирса. Пирс, сотрудничавший с коллегами в Обсерватории Гарвардского колледжа, поручал Чандлеру проводить математические вычисления. После окончания школы Чандлер благодаря своим навыкам и умениям получил работу в Службе береговой и геодезической съемки США, где он проводил астрономические измерения долготы и широты. После того как его непосредственный руководитель оставил геодезическую службу, Чандлер ушел в страховой бизнес, но подлинной его любовью всегда оставалась астрономия; благодаря связям в Гарварде он мог проводить измерения в Гарвардской обсерватории.

Чтобы измерить широту, Чандлер использовал визуальный зенитный телескоп, то есть телескоп, спроектированный так, чтобы всегда смотреть строго вверх, в небо; широту можно было определить, измерив относительные положения звезд. Еще во время работы в береговой геодезической службе Чандлер замечал, что правильное горизонтальное выравнивание телескопа требует больших усилий и почти вдвое увеличивает время, необходимое для измерений. Поэтому в качестве своего первого проекта в роли астронома-любителя он создал новое устройство, способное выравниваться самостоятельно, и назвал его альмукантаром. С середины 1884-го по середину 1885 г. Чандлер испытывал точность альмукантара в Обсерватории Гарварда; его измерения неожиданно показали, что существует непрерывное систематическое изменение широты Обсерватории на протяжении года. Это и были первые измерения свободной нутации. Сам Чандлер не стал рассуждать об их происхождении; он отметил только, что не смог найти источник ошибки, которой можно было бы объяснить эти наблюдения.

Вопрос этот вполне мог бы оставаться нерешенным еще много лет, если бы не замечательное совпадение: почти в тот же период, когда Чандлер делал свою работу, немецкий ученый Фридрих Кюстнер из Берлинской обсерватории также наблюдал отклонения широты. Кюстнер, как и Чандлер, пытался изучать нечто совершенно другое: в случае Кюстнера это были вариации скорости света, приходящего к Земле от далеких звезд. Позже было показано, что любые подобные усилия обречены, поскольку из специальной теории относительности Эйнштейна следует, что скорость света одинакова везде и всегда, для любого, кто не поленится ее измерить. Так что Кюстнер, что не удивительно, никаких вариаций скорости света не обнаружил и никак не смог объяснить полученные при измерениях вариации широты; дело кончилось тем, что он почти на два года отложил свою работу. Когда же, наконец, в 1888 г. дело у него дошло до публикации результатов, то подтолкнуло его к этому, вполне возможно, именно знакомство с работой Чандлера.

Чандлер, в свою очередь, увидел результаты Кюстнера и понял, что вариации широты, которые он получил при измерениях, представляют собой вполне реальный эффект. Он удвоил усилия в работе с альмукантаром и в 1891 г. опубликовал первые две статьи о чандлеровских колебаниях; в статьях он показал колебания положения точки Северного полюса примерно на 9 м с периодом 427 суток^{6}.

Похоже, Чандлер открыл эти колебания там, где другие потерпели неудачу, просто потому, что не знал, что именно ищет. До него астрономы, охотившиеся за свободной нутацией, сосредотачивались на Эйлеровой оценке периода в 306 суток и не обращали внимания на любые более долгопериодические изменения, считая их сезонными колебаниями в атмосфере, которые действительно способны в принципе менять видимое положение звезд. Но Чандлер, не знакомый с результатом Эйлера, просто измерял, не имея перед собой никакой заранее поставленной цели.

Результаты Чандлера были вполне убедительными. Он не только использовал большой массив собственноручно полученных измерительных данных, но и показал, что данные Кюстнера согласуются с его собственными; мало того, он показал также, что наблюдения из Пулково в России и Вашингтона в США показывают те же колебания.