Загадка падающей кошки и фундаментальная физика

Импульс объекта, определяемый как «(масса) × (скорость)», можно приблизительно описать как количество в объекте «живости». Если два объекта движутся с одинаковой скоростью, но имеют разные массы, то объект с большей массой обладает и бóльшим импульсом; если два объекта имеют равные массы, но движутся с разными скоростями, то объект с большей скоростью обладает и бóльшим импульсом. Когда на дороге сталкиваются легковая машина и грузовик, то грузовик, как правило, давит легковушку, поскольку обладает большей массой и обычно имеет больший импульс.

Из законов Ньютона косвенно следует, что в любой изолированной физической системе импульс сохраняется. Первый закон Ньютона гласит, что скорость объекта не меняется, если на него не действует внешняя сила; следовательно, импульс изолированного объекта не может спонтанно измениться. Поскольку ускорение объекта — это скорость изменения его скорости, то, согласно Второму закону Ньютона, сила соответствует изменению импульса. Третий закон Ньютона гласит, что если импульс одного из взаимодействующих объектов изменяется, то импульс второго должен измениться в точности противоположным образом — так, чтобы суммарный импульс системы остался прежним.

Для демонстрации закона сохранения импульса часто используют бильярдные шары. Если биток послать кием точно в восьмой шар, то биток остановится, а восьмой шар продолжит его движение в том же направлении и с той же скоростью; при этом импульс битка будет полностью передан восьмому шару.

Импульс, который нередко называют линейным импульсом, следует отличать от третьей величины, которая тоже подчиняется закону сохранения: момента импульса, или углового момента. Момент импульса представляет, условно говоря, сколько «живости» имеет объект во вращательном движении; под вращательным движением подразумевается и просто вращение, как у велосипедного колеса, и обращение вокруг некоторого центра, к примеру Земли вокруг Солнца. Для точечной массы момент импульса можно найти по формуле «момент импульса = (радиус) × (масса) × (скорость)», где радиус — радиальное расстояние, на котором объект обращается вокруг точечной массы. Отсюда видно, что, если два объекта имеют равную массу и скорость, но обращаются вокруг центра на разных расстояниях, тот из них, что описывает бóльшую окружность, будет обладать бóльшим моментом импульса.

Для неточечного вращающегося объекта из приведенной формулы следует, что момент импульса зависит не только от массы объекта, но и от распределения этой массы внутри объекта. То и другое вместе вызывает сопротивление вращению, называемое моментом инерции. Если имеется три колеса равной массы, то колеса с бóльшим диаметром (и массой, расположенной дальше от оси вращения) будут обладать бóльшим моментом инерции; именно поэтому проще проехать большое расстояние на велосипеде, чем на роликах: крохотные и легкие колесики роликов теряют момент импульса из-за трения намного быстрее, чем большие и более тяжелые колеса велосипеда. В терминах момента инерции момент импульса вращающегося объекта вычисляется как «момент импульса = (момент инерции) × (радиан в секунду)».

Момент импульса — это, как мы уже говорили, сохраняющаяся величина. Если начать с колеса в покое и закрутить его по часовой стрелке, то для того, чтобы полный момент импульса системы остался равным нулю, что-то другое должно раскрутиться против часовой стрелки. Это хорошо можно продемонстрировать в обычном вращающемся офисном кресле: если резко развернуть тело влево, кресло повернется вправо; момент импульса сохранится.

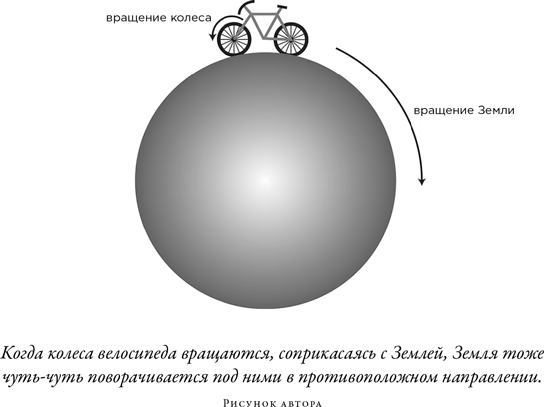
Из закона сохранения момента импульса следует несколько довольно странных вещей. Когда велосипедист нажимает на педали, момент импульса, передаваемый на колеса, уравновешивается равным противоположно направленным моментом импульса, который передается Земле: каждый велосипедист чуть-чуть раскручивает Землю! Земля так велика и массивна (она обладает таким высоким моментом инерции), что реальное вращение, передаваемое ей таким образом, пренебрежимо мало. Более того, по всей Земле в самых разных направлениях ездит столько велосипедов, что в среднем все эти крохотные вращения, по существу, компенсируют друг друга.

Намек на идею момента импульса можно найти уже в Ньютоновых «Началах», где он, по крайней мере, признает существование своеобразной «инерции вращения», аналогичной обычной инерции, которая описывается его Первым законом движения. Как утверждается во введении к Первому закону: «Волчок, части которого, связанные между собой, постоянно увлекает сила прочь с прямолинейного пути движения, не прекращает вращения, за исключением того что тормозится воздухом. Более крупные тела планет и комет, встречая меньше сопротивления в более свободных пространствах, сохраняют свое движение, как поступательное, так и вращательное, на протяжении гораздо более длительного времени»^{3}.

Еще до Ньютона астроном Иоганн Кеплер продемонстрировал при помощи планетарных наблюдений так называемую теорему площадей, согласно которой любая планета движется с большей скоростью, если ее орбита проходит ближе к Солнцу, и с меньшей, если она располагается дальше. Вспомнив, что «момент импульса = (радиус) × (масса) × × (скорость)», мы можем заключить, что если момент импульса сохраняется, а радиус уменьшается, то скорость должна увеличиться. За полтора столетия после Ньютона физики постепенно поняли: из теоремы площадей прямо следует, что существует какой-то общий закон сохранения вращательного момента. К 1800 г. в ученой среде сложилось прочное ощущение, что «момент вращения» сохраняется; наконец, в 1858 г. Уильям Дж. М. Рэнкин в своем «Руководстве по прикладной механике»^{4} ввел для этой величины термин «угловой момент»[1].

Одно простое — но, как мы увидим, обманчивое — следствие из предыдущего обсуждения состоит в том, что момент импульса и вращение непосредственно связаны друг с другом. Рассматривая в качестве примера такой объект, как велосипедное колесо, мы можем сказать, что у него есть момент импульса, когда оно вращается, и нет момента импульса, когда оно не вращается. Из сохранения момента импульса, кажется, следует, что объект, который в начальный момент не вращается, не может ни с того ни с сего начать вращаться. В частности, кошка, которая начинает падение без всякого начального вращения, не может, согласно этим рассуждениям, перевернуться, поскольку это означало бы, что она нарушила закон сохранения момента импульса. Хотя кошачьи энтузиасты, такие как Уильям Гордон Стейблс, продолжали использовать объяснение переворачивания кошки, данное Антуаном Параном в 1700 г., физики конца XIX в. признавали, что Паран ошибался: кошка не должна спонтанно переворачиваться. Они делали вывод, что кошке необходимо в момент начала падения оттолкнуться от любого неподвижного объекта, который подвернется под лапу, — подоконника, с которого она падает, или руки, которая ее роняет, — и таким образом набрать некоторый момент импульса, который позволит ей перевернуться.

Фотографии Марея ясно показали, что эта общепринятая гипотеза неверна. Описание жаркой дискуссии по этому поводу появилось во французском журнале «Домашняя радость» (La Joie de la Maison) под заголовком «Средоточие научной мысли!»^{5}. Приведу здесь эту заметку целиком:

Академия наук посвятила одно из своих недавних заседаний забавному вопросу о том, почему кошка, подобно многим политикам, всегда приземляется на лапы.

Этот вопрос, принадлежащий к числу тех природных явлений, которые приводят в уныние уже тем, что остаются необъясненными, привел Академию в сильное волнение.

К другим примерам таких явлений можно причислить трудный вопрос о том, почему у цыплят нет зубов; или почему, когда два человека — один высокий, другой маленького роста — встречаются на дороге в дождливый день, то именно тот, что поменьше, всегда пытается поднять свой зонт выше зонта рослого человека.

Именно в таком духе мистер Марей представил на внимательное рассмотрение ученым мужам 60 фотографических изображений кошки, которую уронили с высоты полутора метров. На фотографиях видно, как кошка падает с лапами, болтающимися в воздухе, а затем переворачивается, успевая выровняться и приземлиться на все четыре конечности.

«Вот так чудо!» — могли бы вы воскликнуть, зная, как давно уже известно всему миру, что, когда кошка падает, она всегда приземляется прямо на лапы.

Разумеется, всякий это знает; но обычный человек удовлетворяется простым знанием этого факта и не испытывает никакого желания разбираться глубже. Мистер Марей, а заодно с ним и Академия, потребовали большего. Их вопрос был сформулирован следующим образом:

«Почему падающая кошка всегда приземляется на лапы?»

Веселый сарказм автора заметки буквально бросается на читателя с журнальной страницы — и не напрасно: ведь простая задача о падающей кошке привела престижную Академию в состояние полной неразберихи.

Вот тут-то мои дражайшие ученые мужи пустились во все тяжкие. Мистер Марсель Депре указал, что падающее тело не может быть развернуто без приложения внешней силы. Среди других выступивших по этому вопросу были мистер Лоуи, директор Обсерватории, которому, возможно, полезнее было бы наблюдать падающие звезды, а не падающих кошек; мистер Морис Леви, Инспектор по Шахтам (обратите внимание: вовсе не Инспектор по Кошачьим); и мистер Бертран, Постоянный Секретарь Академии наук.