Ответ: кошка, охваченная внезапно своеобразным природным страхом, изгибает спинной хребет, выпячивает живот и вытягивает лапы и голову, как будто пытаясь вернуться назад, в то место, откуда падает, что обеспечивает лапам и голове больший рычаг. При этом необычайном движении центр тяжести кошки поднимается выше геометрического центра фигуры, но, поскольку его там ничто не удерживает, вскоре опускается вновь. Опускаясь, центр тяжести переворачивает кошку животом, головой и лапами к земле. Таким образом, в конце своего падения кошка оказывается на земле на четырех лапах и становится, короче говоря, еще более самодовольной{6}.
Самую полную информацию о рассуждениях Стейблса можно найти во французском «Словаре пословиц, их происхождения, истории и анекдотов, связанных с ними» 1842 г. Там приведена пословица «Он как кошка, которая всегда приземляется на лапы»{7}. В книге пословиц приведено имя настоящего автора рассуждений о переворачивании кошки: это Антуан Паран, почти забытый французский математик. Именно он в 1700 г. опубликовал первое в мире физическое объяснение кошачьей загадки.
Антуан Паран родился в Париже в 1666 г. и уже в раннем детстве проявил себя как математический вундеркинд. В три года мальчика отправили в деревню, где он должен был жить с дядей Антуаном Малле, приходским священником, известным как хороший богослов и талантливый натуралист. Малле обнаружил в юном Паране ненасытное любопытство ко всему, что связано с математикой, и снабдил мальчика всеми книгами по этому предмету, какие только сумел достать. Паран изучил эти книги и сумел самостоятельно разобраться в них и освоить многие математические доказательства. К 13 годам он успел заполнить поля многих книг заметками и комментариями.
Вскоре Антуана принял в ученики друг семьи, преподававший риторику в Шартре. У этого учителя в комнате имелась модель, на которой показывалось, как следует проектировать солнечные часы в разных местах земного шара и чем такие часы должны отличаться друг от друга. Модель имела форму додекаэдра — правильного геометрического многогранника с 12 гранями. На каждой грани додекаэдра были изображены солнечные часы, пригодные для соответствующего региона Земли. Паран, завороженный тонкостью и изяществом конструкции, попытался вывести для них собственные математические закономерности. Попытка не удалась — что не удивительно в 14 лет, — но учитель объяснил юноше, что правильная конструкция солнечных часов определяется сферической геометрией Земли. После этого бесстрашный Паран задумал написать собственное любительское пособие по искусству изготовления солнечных часов, или гномонике.
Парана, хотя страстью его была математика, ждала судьба многих блестящих художников и ученых: друзья убедили его отправиться в Париж учиться на юриста, поскольку юридическое поприще тогда, как и сейчас, было куда более прибыльным, чем математика. Однако сразу же по окончании обучения на юриста Паран заперся в своей комнате в колледже Дорман-Бовэ в Париже и, кое-как сводя концы с концами на нищенский доход, отдался изучению математики. За пределы учебного заведения он выходил только с целью посещения Королевского колледжа Парижа, где можно было пообщаться с коллегами и послушать лекции видных ученых, таких как математик Жозеф Совёр, изучавший геометрию и теорию звука.
Паран был предприимчив, и начало Девятилетней войны между Францией и Аугсбургской лигой европейских государств дало ему возможность пополнить свой бюджет доходами от преподавания. Конфликт породил высокий спрос на солдат и ученых людей, способных разобраться в математике и машинерии военного дела, и Паран набрал учеников, чтобы преподавать им теорию строительства оборонительных сооружений. Сам он, правда, не имел опыта в этом деле; Паран, несомненно, привлек к делу некоторое количество старых книг на эту тему, таких как «Искусство фортификационных сооружений» (La Fortification Démonstrée et Réduicte en Art Жана Эррара выпуска 1600 г.){8}.
Позже, однако, Паран начал испытывать угрызения совести по поводу преподавания предмета, в котором не имел никакого практического опыта. Он рассказал о своей тревоге Жозефу Совёру, и тот предложил молодому человеку помощь в виде рекомендации для устройства на работу. При посредничестве Совёра Паран был представлен маркизу д’Алигру — аристократу, принимавшему участие в Девятилетней войне и как раз нуждавшемуся в услугах математика. Под началом д’Алигра Паран побывал в двух военных кампаниях, что принесло ему репутацию блестящего ученого, математика и мыслителя.
В 1699 г. Паран смог воспользоваться собственной репутацией к немалой своей пользе. В том году математик Жиль Фийо дес Бийет был принят в Королевскую академию наук в Париже в завидной роли «механика», и он взял себе учеником Парана, заработавшего к тому времени широкую известность и авторитет. Паран, получивший таким образом стабильное положение в академическом мире, начал в свое удовольствие заниматься ошеломляюще разнообразными исследованиями в самых разных областях, включая анатомию, ботанику, химию, математику и физику. Однако неиссякаемый энтузиазм и неуемная натура теперь стали работать против него.
Но эта широта знаний вкупе с природной горячностью и порывистостью нрава породили в нем дух противоречия, которому он неизменно следовал, иногда с поспешностью, заслуживавшей величайшего осуждения, и часто почти без оглядки на благопристойность. На самом деле к себе он стал встречать такое же отношение, и труды, которые он представлял ученому миру, часто ждал суровый прием. Его произведения обвиняли в непонятности; мало того, этот недостаток был настолько известен, что он и сам его видел и никак не мог уклониться от исправления.
Этот отрывок, взятый из математического словаря 1795 г., представляет собой, по существу, перевод посвященной Парану памятной записки, составленной его коллегами — членами Парижской академии после смерти ученого{9}. Коллеги считали отношение Парана к окружающим настолько возмутительным, что сочли нужным увековечить его ни много ни мало в некрологе.
Тем не менее Паран регулярно докладывал о своих результатах ученому сообществу, которое вплоть до его смерти столь же регулярно публиковало их изложение в своем журнале
В статье Парана речь идет о плавучести объектов, погруженных в воду. Еще в 250 г. до н. э. греческий философ и математик Архимед первым объявил, что выталкивающая сила, действующая на погруженный объект, равна весу воды, вытесненной этим объектом. Таким образом, на любое погруженное тело действуют две силы: сила тяготения, тянущая его вниз, и сила выталкивания, толкающая его вверх. Если объект тяжелее той воды, которую он вытесняет, он утонет; если легче, будет плавать.
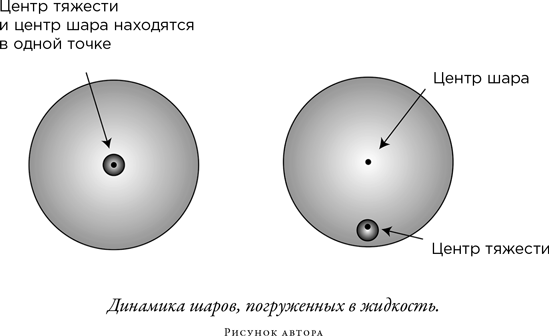
Плотность воды в глубоком водоеме увеличивается с глубиной, а значит, вес фиксированного объема воды тем больше, чем глубже этот объем находится. Поэтому деревянный шар, который весит меньше, чем эквивалентный ему сферический объем воды на поверхности водоема, будет вытолкнут наверх и закачается на поверхности; свинцовый шар, весящий больше, чем эквивалентный ему сферический объем воды вблизи дна водоема, утонет и опустится на дно. Но если мы изготовим шар, представляющий собой небольшой свинцовый сердечник в деревянной оболочке, как показано на рисунке слева, то можно так подобрать размер сердечника, чтобы объект в целом погрузился в воду и «завис» на некоторой глубине под поверхностью воды; он там «парит», говоря словами Парана.
Но что, если шар сделать асимметричным: вставить свинцовый сердечник в стороне от геометрического центра деревянного шара, как показано на правом рисунке? Тогда центр тяжести комбинированного шара окажется не в его центре, а ближе к свинцовому сердечнику. Каким будет поведение этого шара в сравнении с поведением шара с центральным сердечником?
Данный вопрос на тот момент был уже рассмотрен: сделал это за несколько десятилетий до Парана итальянский физик Джованни Альфонсо Борелли в своем двухтомном труде 1685 г. De Motu Animalium — «Движение животных». Борелли интересовался изучением различных движений животных и составляющих их мышц средствами математики и физики. Благодаря важным исследованиям в этой области и твердому убеждению, что животных можно рассматривать как сложные автоматы, Борелли сегодня часто называют «отцом биомеханики».
К исследованию задачи плавания шара в жидкости Борелли подтолкнул интерес к тому, как двигаются в воде животные. Рассматривая случай неравномерно плотного шара, Борелли утверждал, что если такой шар будет падать с высоты в толщу воды тяжелой стороной кверху, то сначала он опустится до уровня, где силы плавучести и тяготения уравновешивают друг друга, и только
Паран считал, что движение в этом случае происходит по более сложной схеме. У него было преимущество: за прошедшие годы появилась более продвинутая физика, при помощи которой он мог обосновать свои выводы. Основополагающая книга Исаака Ньютона «Математические начала натуральной философии» (Philosophiae Naturalis Principia Mathematica), которую часто называют просто «Начала», была опубликована в 1687 г., через пару лет после работы Борелли, и в ней впервые была представлена единая математическая теория движения массивных тел. Воспользовавшись некоторыми откровениями Ньютона, Паран заметил, что сила тяжести и сила плавучести должны действовать на разные точки шара. Выталкивающая сила должна тянуть вверх и действовать в геометрическом центре шара, а сила тяжести — тянуть вниз и действовать в центре тяжести. Из-за того что силы приложены в разных местах, рассуждал Паран, шар неизбежно будет поворачиваться вокруг некоторой точки, расположенной между двумя этими центрами, а сам поворот будет происходить еще в процессе спуска шара к равновесной глубине.
Объект, вращающийся в процессе падения, сильно напоминает падающую кошку, и Паран, очевидно, думал так же. Выложив свои математические аргументы, он заметил:
Следовательно, кошки и некоторые другие животные того же сорта, как куницы, хорьки, лисы, тигры и т. п., когда падают с возвышенного места, обычно падают на лапы, хотя сначала их лапы были выше тела, и животные вследствие этого упали бы на голову. Они, совершенно определенно, не смогли бы сами перевернуться в воздухе, где у них нет неподвижной точки опоры, чтобы опереться. Но страх, который они испытывают, заставляет их сгибать спинной хребет, так что их брюхо выталкивается вверх, и одновременно вытягивать голову и ноги к тому месту, откуда произошло падение, как будто пытаясь до него дотянуться, что дает эти частям, как рычагам, выигрыш в силе. Таким образом, центр тяжести животного смещается по отношению к центру фигуры, причем смещается вверх, из чего следует, согласно демонстрации месье Парана, что эти животные должны совершить полупереворот в воздухе, обратив ноги вниз, что почти всегда спасает им жизнь. Наилучшее знание механики не окажется полезнее в этом случае, чем знание путаной и невнятной поэзии.
Физики с давних пор печально известны тем, что пытаются решать задачи путем упрощения их до такой степени, что они приобретают до нелепости неузнаваемый вид. Среди студентов-физиков с давних времен бытует шутка о том, что физик начинает моделирование коровы с фразы: «Для простоты представим себе, что корова имеет сферическую форму в вакууме». Паран в своей работе сделал почти буквально подобное упрощение, предложив рассматривать падающую кошку как парящую в воздухе сферу.