Теорема века. Мир с точки зрения математики
– равна двум прямым в геометрии Евклида;
– меньше двух прямых в геометрии Лобачевского;
– больше двух прямых в геометрии Римана.
Число линий, которые можно провести через данную точку параллельно данной прямой:
– равно единице в геометрии Евклида;
– нулю в геометрии Римана;
– бесконечности в геометрии Лобачевского.
Прибавим, что пространство Римана конечно, хота и безгранично, в указанном выше смысле этих двух слов.
Поверхности с постоянной кривизной. Остается возможным одно возражение. Действительно, теоремы Лобачевского и Римана не содержат никакого противоречия; но как бы ни были многочисленны следствия, которые вывели из своих допущений эти два геометра, все же последние должны были остановиться, не исчерпав всех возможных выводов, потому что число их бесконечно. Но тогда кто поручится, что если бы они продолжали свои выводы далее, то все же не пришли бы к противоречию?
Это затруднение не существует для геометрии Римана, если ограничиваться двумя измерениями; в самом деле, геометрия Римана для двух измерений не отличается, как мы видели, от сферической геометрии, которая есть только ветвь обыкновенной геометрии и которая, следовательно, стоит вне всякой дискуссии.
Бельтрами, сведя также и геометрию Лобачевского для двух измерений к тому, что она стала только ветвью обыкновенной геометрии, опроверг таким же образом направленное против нее возражение. Вот как он пришел к этому. Рассмотрим на некоторой поверхности произвольную фигуру. Представим себе, что эта фигура начерчена на гибком и нерастяжимом полотне, наложенном на эту поверхность, так что, когда полотно перемещается и деформируется, различные линии этой фигуры могут изменять форму, не меняя длины. Вообще, эта гибкая и нерастяжимая фигура не может перемещаться, не оставляя поверхности; но есть некоторые особые поверхности, для которых подобное движение было бы возможно: это поверхности с постоянной кривизной.
Возвратимся к сравнению, которое мы сделали выше, и вообразим себе существа без толщины, живущие на одной из таких поверхностей. Движение фигуры, все линии которой сохраняют постоянную длину, с их точки зрения будет возможно. Подобное движение, наоборот, казалось бы абсурдным для существ без толщины, живущих на поверхности с переменной кривизной.
Поверхности с постоянной кривизной бывают двух родов. Одни из них – поверхности с положительной кривизной; они могут быть деформированы так, что накладываются на сферу. Следовательно, геометрия этих поверхностей сводится к сферической геометрии, которая есть геометрия Римана. Другие – поверхности с отрицательной кривизной. Бельтрами показал, что геометрия этих поверхностей есть не что иное, как геометрия Лобачевского. Таким образом, геометрии двух измерений, как Римана, так и Лобачевского, оказываются связанными с евклидовой геометрией.
Истолкование неевклидовых геометрических систем. Таким образом, устраняется возражение, касающееся геометрических систем двух измерений.
Легко было бы распространить рассуждение Бельтрами на геометрии трех измерений. Умы, не отрицающие пространства четырех измерений, не увидят в этом никакой трудности, но таковых немного. Поэтому я предпочитаю поступить иначе.
Возьмем некоторую плоскость, которую я буду называть основной, и построим нечто вроде словаря, установив соответствие в двойном ряду членов, написанных в двух столбцах, таким же образом, как в обычных словарях соответствуют друг другу слова двух языков, имеющие одинаковое значение.
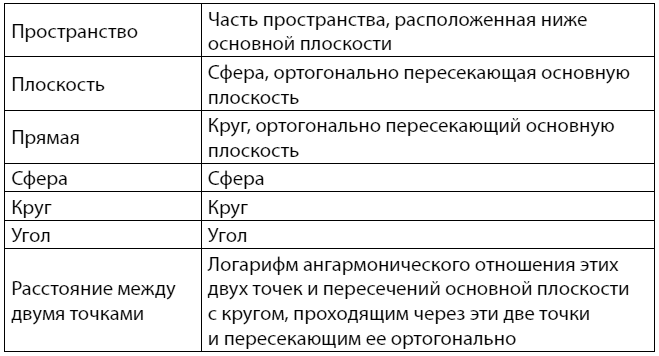
И т. д.
Возьмем затем теоремы Лобачевского и переведем их с помощью этого словаря, как мы переводим немецкий текст с помощью немецко-французского словаря. Мы получим таким образом теоремы обыкновенной геометрии.
Например, теорема Лобачевского: «сумма углов треугольника меньше двух прямых» переводится так: «если криволинейный треугольник имеет сторонами дуги кругов, которые при продолжении пересекают основную плоскость ортогонально, то сумма углов этого криволинейного треугольника будет меньше двух прямых». Таким образом, как бы далеко мы ни развивали следствия из допущений Лобачевского, мы никогда не натолкнемся на противоречие. В самом деле, если бы две теоремы Лобачевского находились в противоречии, то то же самое имело бы место и для переводов этих двух теорем, сделанных при помощи нашего словаря; но эти переводы суть теоремы обыкновенной геометрии, а никто не сомневается, что обыкновенная геометрия свободна от противоречий. Однако откуда происходит в нас эта уверенность и справедлива ли она? Это – вопрос, который я не буду разбирать здесь, так как он потребовал бы подробного развития. Во всяком случае, указанное выше возражение отпадает полностью.
Это еще не все. Геометрия Лобачевского, допускающая таким образом конкретное истолкование, перестает быть пустым логическим упражнением и может получить применение; я не имею времени говорить здесь ни об ее приложениях, ни о той пользе, которую Клейн и я извлекли из нее для интегрирования линейных уравнений.