Сначала сигнал разбили на последовательность дискретных единиц, каждую из которых маркировали числом, описывающим амплитуду волны в конкретный момент. Это позволило им добавлять к передаче случайные числа, известные только отправителю и получателю сигнала. Теперь для перехватчика стало математически невозможно получить доступ к информации.
Работая над “системой X”, Шеннон увлекся технологиями шифрования. Он даже беседовал о них с британским математиком Аланом Тьюрингом, который участвовал во взломе немецкого шифра “Энигма” и в 1943 году посетил Лаборатории Белла, чтобы изучить американские инновации в области шифрования. Как выяснилось, взгляды Тьюринга и Шеннона на оптимальные способы шифрования не совпадали, поэтому в своих разговорах за чаем они почти не затрагивали рабочих тем, а рассуждали о том, какими возможностями могут обладать компьютеры. Они сошлись во мнении, что компьютеры теоретически могут имитировать работу человеческого мозга и что на реализацию этого на практике уйдет пара десятков лет. Очевидно, эта идея не давала Тьюрингу покоя и после войны, поскольку в 1948 году он написал революционную статью “Разумные машины”[213]. Шеннон, однако, отвлекся. Его прорывная статья 1948 года называлась “Математическая теория связи”[214]. Построив ее на базе своей выдающейся магистерской диссертации, он подробно описал в ней все, что произойдет в технологиях связи в последующие семьдесят лет.
Первый элемент статьи Шеннона – идея о том, что информацию можно моделировать на основе статистического подхода. Шеннон отмечает, что одни комбинации слов более вероятны, чем другие: например, вы вряд ли ожидаете, что после слова “стол” я поставлю слово “депресняк”. Мы воплотили это в умной (но далеко не безупречной) технологии интеллектуального ввода текста на наших телефонах, но именно Шеннон первым продемонстрировал, что благодаря этому у нас появляется возможность для более эффективной коммуникации. По сути, это позволяет “сжимать” многие формы коммуникации. Например, мы можем отказаться от передачи некоторых фрагментов информации, поскольку человек, выступающий получателем, сумеет без труда их восстановить. Английский язык прекрасно подходит для этой задачи: его гласные часто избыточны. Как Шеннон отметил в статье для “Британской энциклопедии”, MST PPL HV LTTL DFFCLTY N RDNG THS SNTNC[215].
Второй элемент – идея об информационной энтропии. Шеннон зацепился за возможность оцифровки сигнала с целью сведения его к последовательности поддающихся манипуляции чисел. Он также нашел способ количественного представления информации, содержащейся в сигнале, что интересовало и Тьюринга. Тьюринг назвал единицу информации “бан”, но Шеннон выбрал вариант, предложенный коллегой в конце 1946 года, когда они обменивались идеями за обедом. Двоичная единица не может называться “баном”, “биджитом” или “бинитом”, сказал Джон Тьюки. “Разве не очевидно, что ее нужно назвать бит?”[216]
Но как понять, сколько у вас битов? Здесь Шеннон оттолкнулся от малоизвестной работы инженера Ральфа Хартли. Хартли более десяти лет проработал в
Логарифм по основанию 2 от 17 576 равен 14,1. Это значит, что для передачи английского трехбуквенного слова нам нужно сделать выбор не более 15 раз. Иными словами, размер сообщения составляет 15 бит.
Глядя на биты, можно увидеть, как происходит взаимодействие между ними. Один бит дает нам только два варианта: 0 или 1. Два бита дают четыре варианта: 00, 01, 10, 11. Три бита дают восемь вариантов: 000, 001, 010, 011, 100, 101, 110, 111.
Четыре бита дают 16 вариантов. Можно также повернуть счет с ног на голову и сказать, что в процессе выбора одного из 16 одинаково вероятных сообщений задействуется четыре бита информации. Здесь наблюдается логарифмическая связь: 4 – это логарифм по основанию 2 от 16.
В общем виде правило таково: при наличии
Чтобы проиллюстрировать это, вернемся к примеру с подбрасыванием правильной монеты. Оба исхода – орел и решка – имеют одинаковую вероятность: 1 к 2, или 0,5. Логарифм по основанию 2 от 0,5 равен –1. Для варианта “орел” умножим его на 0,5 и на –1. Затем поступим так же с вариантом “решка”. Сложим результаты. Это даст нам 1 бит энтропии Шеннона – объем информации, заключенной в подбрасывании монеты.
В другой части своей статьи Шеннон обратился к иному наблюдению Хартли: о том, что значение имеет и канал связи. Если канал позволяет использовать широкий диапазон частот – например, если он “широкополосный”, – в сообщении получится уместить больше деталей, а следовательно, у вас будет больше вариантов, что позволит вам передать больший объем информации за отведенное время. На основе этого Шеннон вывел математику “пропускной способности канала”. Он показал, что можно охарактеризовать используемый для передачи информации канал, назвав максимальное число битов, которые можно гарантированно загружать в него (и считывать с него) каждую секунду. Приведу пример (хотя и упрощенный): пропускная способность
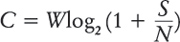
Пропускная способность канала измеряется в битах в секунду – а лучше, конечно, в миллионах бит (мегабитах) в секунду, если измерять приходится пропускную способность вашего интернет-соединения. Именно поэтому широкополосный доступ в интернет лучше старой технологии доступа через телефонный модем: он создает более широкую полосу пропускания и увеличивает
Четвертый важный вклад в науку Шеннон сделал, показав, как работать с ошибками, которые возникают при передаче данных. Отправляя сигнал, вы можете столкнуться с помехами – случайными внешними факторами, – которые не позволят получателю прочитать и расшифровать пришедшие к нему биты.
Эта проблема возникает не только в сфере высоких технологий: представьте, что вы общаетесь с помощью светового кода в Древнем Риме – например, двигаете зеркало, чтобы систематически отражать солнечные лучи в сторону союзной армии, стоящей на соседнем холме. Если свет упадет на чей-нибудь щит, в вашем сообщении появится ложный бит. Сегодня, когда вы передаете HTML-код веб-страницы по медному проводу, подобное может спровоцировать случайный электрический сигнал от удара молнии или случайное колебание в одном из компонентов электрической схемы. Оптоволоконный кабель, по которому телевизионный сигнал передается в форме отдельных световых импульсов, тоже может терять часть фотонов – сгустков энергии света – с важнейшими битами информации. Но переживать не стоит, ведь Шеннон о вас позаботился.
Можно подумать, что у этой проблемы есть очевидное решение, которое не требует вмешательства Шеннона: достаточно всего лишь передать сигнал дважды. Это, несомненно, неплохая идея. Если два сигнала совпадут, можно с высокой степенью уверенности сказать, что вы получили верное сообщение, поскольку маловероятно, что одинаковое случайное вмешательство (или случайная потеря) произошло дважды. Но так передача замедлится, а расход энергии возрастет. Шеннон показал, что в этом нет необходимости.
В его статье есть раздел о “кодировании каналов”, где он утверждает, что, зная, с какими помехами вам предстоит столкнуться, вы можете разработать такую систему кодирования, которая обеспечит вам математически идеальную коммуникацию. Допустим, я хочу передать четыре фрагмента информации. Чтобы различать их, я присвою им “кодовые имена”, состоящие из пар двоичных символов:
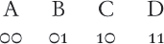
При передаче по каналу с помехами, которые будут время от времени отнимать биты, возникнет риск, что получатель увидит B там, где я имел в виду A, или D там, где я имел в виду C. Что, если передать каждый фрагмент дважды? Тогда C превратится в 1010, но при изменении одного бита из-за помехи может получиться 1011. Будет казаться, что я передал либо С, либо D, – и сделать выбор будет невозможно.
Я мог бы передавать каждый фрагмент по три раза. Теперь C будет 101010, и изменение одного бита даст 111010, 100010 или 001010. Какой бы бит ни изменился, большинством голосов (2 к 1) можно постановить, что я хотел передать 10.
Шеннон, однако, показал, что у нас есть способ получше: хотя это и не очевидно, нам достаточно передавать лишь пять битов, при условии, что мы тщательно оформим закодированные слова таким образом, чтобы сделать “расстояние” между ними максимальным. В нашем примере шифрование должно осуществляться так:
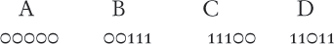
Здесь случайная замена одного бита не вызовет вопросов о том, какой именно фрагмент информации пытались передать. Попробуйте! На удивление – а это удивило всех, – Шеннон показал, что можно найти оптимальную схему кодирования для любого канала с шумами. Иными словами, всегда существует корректирующий код, позволяющий передавать данные, используя почти всю пропускную способность канала (сегодня этот закон часто называют пределом Шеннона для безошибочной передачи данных). К несчастью, аргумент Шеннона был вероятностным. Шеннон не дал никакого способа понять, какие кодовые комбинации позволяют достичь предела в различных ситуациях.