Переведя текст, голландский математик потребовал, чтобы в качестве вознаграждения за услугу незнакомец решил задачу. К изумлению Бекмана, юноша принес решение уже на следующее утро — это был Рене Декарт, полк которого в ту пору стоял в Бредах[20]. [7, стр. 105]
Тщательно пытаясь во время вечерней работы проинтегрировать одно сложное уравнение, Анри Пуанкаре сознательно отложил новые попытки до утра и лег спать. Под утро он увидел сон, будто он читает студентам лекцию по теме своих вечерних занятий и легко интегрирует на доске то самое уравнение. Когда ученый проснулся, ему осталось лишь записать решение. [7, стр. 105–106]
После того, как Эмми Неттер была избрана профессором математике в Геттингене, среди ее коллег-мужчин возникли дебаты: может ли женщина присутствовать на заседаниях ученого совета университета? Спор решил Гильберт:
— Разве ученый совет — баня, что на него нельзя допустить женщину? [7, стр. 106] [24, стр. 74]
Автор наиболее широко распространенной теории иррациональных чисел Р.Дедекинд умер 12 февраля 1916 года в возрасте 84 лет.
Однако еще в 1904 году в «Книжке памятных дат для математиков», был отмечен под датой 4 сентября 1899 г… день смерти Р.Дедекинда. Последний не замедлил написать письмо составителю упомянутой книжки примерно следующего содержания: «Глубокоуважаемый коллега! В Вашей содержательной «Книжке памятных дат» Вы любезно вспомнили и обо мне. Я очень благодарен Вам за это. Разрешаю себе, однако, обратить Ваше внимание на то, что в указании даты моей смерти по крайней мере год, должно быть, указан неверно[21]». [7, стр. 106] [24, стр. 93]
В октябре 1903 г. в Нью-Йорке на заседании математического общества слово было предоставлено профессору Коулу. Профессор подошел к доске и, не говоря ни слова, начал возводить 2 в степень 67. Затем он вычел из полученного числа 1, и, по-прежнему не говоря ни слова, столбиком перемножил два числа 193 707 721 и 761 838 257 287. Оба результата совпали. Впервые в истории Американского математического общества его члены бурными аплодисментами приветствовали докладчика. Профессор Коул, так и не проронив ни одного слова, сел на место. Никто не задал ему ни одного вопроса.
Так Коул доказал, что число 267 — 1 составное, а не простое, как это подозревали до него почти 200 лет[22]. [7, стр. 106]
Среди многочисленных лекций о приложениях математики, прочитанных Чебышевым, отмечается и его доклад в Париже, посвященный математической теории в производстве одежды. Собрались лучшие закройщики и модельеры, различные эксперты элегантности. Чебышев начал свою лекцию знаменитой математической фразой: «Допустим, для простоты, что тело человека имеет сферическую форму…».
После таких слов дальнейшая речь звучала в пустом зале, поскольку шокированная публика удалилась. [7, стр. 107]
Известный русский математик М.В.Остроградский долго бился над решением задачи, которая была камнем преткновения для математиков мира.
Однажды, будучи в Париже, он решил обратится за консультацией во Французскую академию наук, славившуюся своими математическими достижениями. Там долго медлили, а потом пришел ответ: «Эту задачу может решить только один человек — русский профессор Остроградский. Он живет в Петербурге. К нему вам и следует обратится». [7, стр. 107] [40, стр. 349–350]
Парижская академия наук объявила конкурс на тему «О распространении волн в цилиндрических бассейнах». За 10 лет не было подано ни одной работы. В то время в Париже проживал выдающийся русский математик М.В.Остроградский. Он слушал лекции у О.Коши, П.Лапласа, Ж.Фурье… Случилось так, что отец не прислал ему вовремя денег, и М.В., задолжавший хозяину гостиницы, попал в долговую тюрьму. Там он и написал ценнейший труд, в котором решил вопрос, поставленный Парижской академией. Когда его, спустя годы, спросили, чему он обязан в решении столь трудной проблемы, М.В. кратко ответил: «Тюрьме!» [7, стр. 107]
Остроградский не любил модной одежды. Прекрасно зная это, портной все же уговорил его сшить костюм по последней моде. Ученый нашел брюки слишком узкими и отказался взять костюм. Портной удивился: «Но я сделал все, как нужно, — уверял он Остроградского. — Вы не должны отставать от века». «Помилуйте, — возразил академик, — как же мне угнаться за веком в таких узких штанах». [7, стр. 107] [24, стр. 224]
Задолго до Менделеева ученые отметили сходство химических свойств некоторых элементов. Английский химик Ньюлендс в 1804 году попытался объединить элементы в тройки, однако не рискнул предположить существование неизвестных элементов. Поэтому в его тройки попали весьма непохожие элементы, что вызвало у оппонента ехидный вопрос: «А не пытался ли почтенный автор располагать элементы по алфавиту и не была ли при этом замечена какая-нибудь закономерность?» [8, стр. 32]
В 1879-м году составитель головоломок Сэмюэль Лойд свел с ума Европу и Америку следующей головоломкой. Дана коробочка из 16-ти полей и 15-ти шашек, одно поле свободно. Требуется перевести коробочку из левого положения в правое
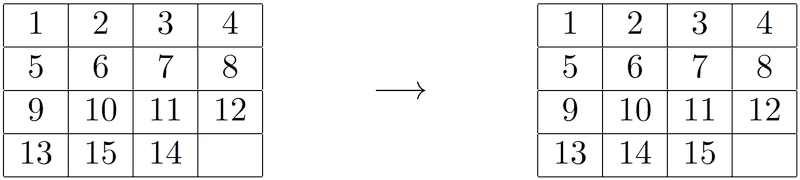
Разрешается передвигать за один ход одну шашку на свободное поле.
За решение задачи была предложена крупная сумма денег. Фабрикант, выпускающий игру, быстро разбогател — священники не выпускали из рук коробочки во время богослужения, машинисты решали головоломку, ведя поезда, торговцы забывали открывать свои магазины…. Горячка прошла лишь после того, как в 1880-м году была доказана неразрешимость задачи Лойда. [8, стр. 43–44]
В 1859-м году сэр Вилльям Роуэн Гамильтон, известный своими глубокими исследованиями по математической физике, теоретической механике и открытием исчисления кватернионов, придумал игру «Кругосветное путешествие» и продал ее за 25 гиней фабриканту игрушек. Утверждают, что эта сумма была единственным заработком, полученным Гамильтоном за свои математические открытия. [8, стр. 60–61]
Швейцарский психолог Жан Пиаже считает, что дети постигают геометрические свойства в обратном порядке[23]. Например, малышу легче понять различие между кучкой красных и кучкой синих шариков (теория множеств) или между замкнутой в кольцо и разомкнутой резиновой лентой (топология), чем отличить пятиугольник от шестиугольника (евклидова геометрия). [9, стр. 73]