Курьёзы и юмор с физико-математическим уклоном

— Нэту его. Кушает, наверное…

Сверху и снизу

ТФКП. У доски студентка. Диктую условие примера

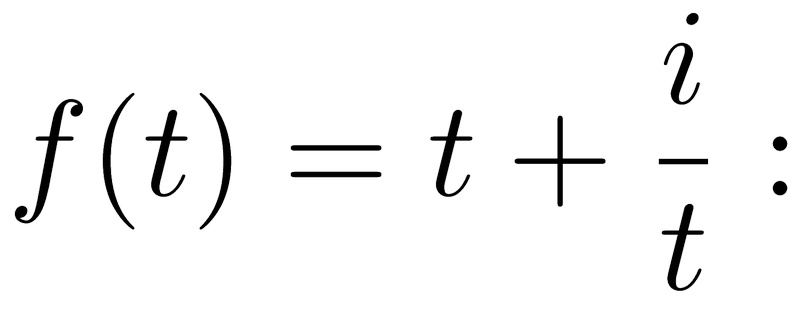
— Эф от тэ равно…

— От чего?

— От тэ (Таня).

Когда записали условие, я не удержался то комментария:

— Вот так, Таня сверху; Таня снизу…

Грааль!

Семинар на кафедре у В.Г.Кротова. Докладывает руководитель семинара Э.И.Зверович. Когда ему задали вопрос, непонятный момент он прокомментировал так:

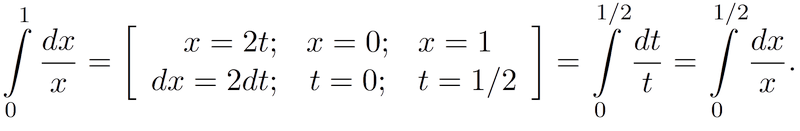
— Интеграл от положительной функции по отрезку равен интегралу от этой же функции по половине отрезка.

Эквидомоид

История от Я.В.Радыно. Одному аспиранту была поставлена задача — построить и изучить правильный многогранник с огромным числом граней (порядка нескольких тысяч). Аспирант многогранник построил и назвал его «эквидомоид». Потом написал про него книгу, которая заканчивалась словами: «Аналитик, будь верен правде, ибо эквидомоид мстителен. И однажды, холодной осенней ночью, он заберется к тебе в душу и съест ее от тоски и грусти…».

Значок ко дню МехМата

Значок ко дню МехМата МГУ — простой кружок, на белом фоне нарисованы два куриных яйца и надпись снизу: «МехМат. Круче только яйца».

Алкогольная аппроксимация

Всем хорошо известно выражение: «сколько бы бутылок водки Вы ни собирались купить, чтобы потом не бегать, сразу берите ровно в два раза больше!»

В.Г.Кротов внес в формулу небольшую поправку: пусть n — количество бутылок спиртного, которое планируется купить на какое-либо мероприятие. Тогда, «чтобы потом не бегать», необходимо купить (2n + 1). Более того. В.Г. выдвинул гипотезу, что, несмотря на то, что формула (2n + 1) дает достаточно хорошую аппроксимацию, пригодную для любых практических целей, истинное соотношение все же сложнее, например:

[еn], где символ [·] обозначает целую часть числа.

Два замечательных студента

Д.О.Пытко отмечал присутствующих методом листика — каждый записывался сам — и последующей переклички. В списке постоянно появлялись два замечательных студента: Травкин Бурьян Бурьянович и Гайкин Шуруп Шурупыч.

Удвоение шара

Теорема Банаха-Тарского об «удвоении» шара утверждает, что замкнутый шар в R³ радиуса R можно разрезать неким «хитрым» способом так, что потом из полученных «кусков» можно составить шар радиуса 2R, причем без пустот внутри. Комментарий Я.В.Радыно:

— Естественно, способ «разрезки» шара явно в теореме не приводится. Потому как если бы я знал этот способ — я бы всю страну обогатил… Что значит как? Взять шар, намазать его маслом, разрезать, сложить шар вдвое большего радиуса и соскоблить масло — все, теперь масла стало в два раза больше!

P.S. мне кажется, что вместо масла, размазанного по шару, лучше взять шар из какого-нибудь драгметалла. Во-первых выгода очевиднее, а во-вторых я тогда подумал: «а вдруг намазанная маслом поверхность после сборки большого шара окажется внутри — мы ведь не знаем способ «разрезки».

Незачетная оценка

Когда минимальной зачетной оценкой вместо трех баллов стала четверка, двоечники возмущались[112]: «Да как же так?! Я всю жизнь только на тройки и учился, а тут вдруг — незачетная оценка!»

Поиграем в снежки?

Практика по математическому анализу (2011), за окном падает слегка неожиданный для марта снег. Диалог со студентами: