Искусство большего. Как математика создала цивилизацию

Найтингейл с детства занималась математикой. Проходя подготовку во Франции и Германии, она собирала больничные выписки, статистические данные и информацию об организации санитарного контроля и ухода за пациентами в госпиталях. Работая в Скутари, она провела учет смертности больных и сравнила данные с показателями смертности в других местах. Оказалось, что в Скутари умирало 37,5 % пациентов, но в госпиталях на линии фронта уровень смертности составлял всего 12,5 %. Вооружившись числами, Найтингейл решила выяснить, почему так происходит, и принять меры. Как? С помощью действенной инфографики.

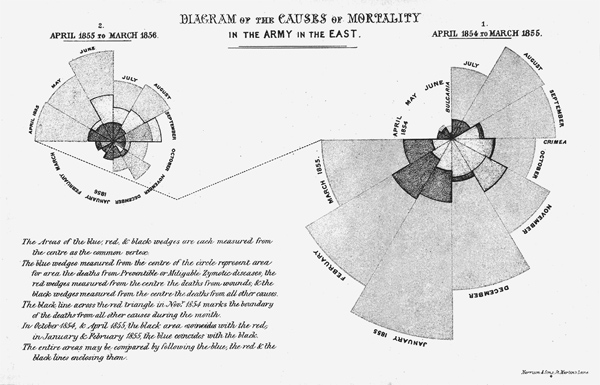
Круговая диаграмма Флоренс Найтингейл. Wellcome Collection, Attribution 4.0 International (CC BY 4.0)

По круговой диаграмме Найтингейл сразу видно, что от болезней на Крымской войне умирало больше солдат, чем от ран. Площадь каждого сектора соответствует месячному уровню смертности, а причины смерти отмечены разными цветами. Найтингейл показала диаграмму военному министру, а затем включила ее в свою книгу “Заметки о факторах, влияющих на здоровье, эффективность и управление госпиталями британской армии”, вышедшую в 1858 году. Экземпляр этой книги она отправила королеве Виктории, которая велела, чтобы Найтингейл явилась к ней на аудиенцию и лично представила свои выводы. В результате она добилась основания Королевской комиссии по проблемам здоровья в армии, что привело к реформам в военной медицине. И ключевую роль в этом, по словам Найтингейл, сыграла диаграмма: “Диаграммы весьма полезны для иллюстрации некоторых аспектов демографической статистики, поскольку они в визуальной форме передают идеи, ухватить которые сложнее, когда у нас перед глазами одни числа”.

Флоренс Найтингейл была не просто сестрой милосердия и не просто статистиком – она была и очень умелым лоббистом. Обретя славу после заметки в Times, она стала пользоваться своим положением. У славы была и обратная сторона – в августе 1856 года Найтингейл пришлось тайком вернуться в Британию под чужим именем, чтобы избежать толп, – и все же слава помогла ей собрать более 40 тысяч фунтов в Фонд Найтингейл, и этого хватило на основание Найтингельской школы подготовки сестер милосердия при больнице Святого Фомы в Лондоне. В довершение всего в 1859 году Найтингейл стала первой женщиной – членом Королевского статистического общества. И приняли ее туда вовсе не из-за славы: так там отметили ее выдающиеся заслуги в сфере, которой она посвятила не один десяток лет.

В поисках значимости

К тому времени, когда Флоренс Найтингейл впервые применила свои диаграммы, статистики уже разработали немало инструментов для анализа данных. Первым был метод построения простейшей кривой, лучше всего описывающей основную тенденцию в наборе разрозненных данных. Этот “метод наименьших квадратов” позволил проводить кривую как можно ближе к каждому из элементов данных, сохраняя при этом плавность.

Математики спорят о том, кто предложил метод наименьших квадратов. Француз Адриен Мари Лежандр опубликовал свою версию в 1805 году, но немец Карл Фридрих Гаусс подробнее описал его в 1809-м (через год после того, как Роберт Эдрейн, школьный учитель из США, опубликовал свой не менее удачный вариант этого метода). Лежандр, Гаусс и Эдрейн вывели формулу, работающую с “отклонениями”, то есть вертикальными расстояниями до кривой от каждого элемента данных. Поскольку точки данных имеются по обе стороны от кривой, одни отклонения положительны, а другие отрицательны, и поэтому сначала нужно возвести их в квадрат, чтобы избавиться от минусов. Кривая наименьших квадратов – это кривая с наименьшей суммой квадратов отклонений.

Гораздо интереснее “нормальное распределение” Гаусса, которое относится к 1809 году. “Распределение” – это разброс данных. Оно бывает разным, и нормальное – или гауссово – распределение формируется в том случае, когда идентичны три определенных характеристики данных. Это среднее значение, мода и медиана. С двумя из них мы встречались, когда изучали работу Фрэнсиса Гальтона, и вместе с модой они дают нам три разных способа вычисления того, что непосвященные называют “средним”.

Представим набор данных, в котором, например, записан рост всех людей, живущих на вашей улице. Чтобы вычислить среднее значение в этом наборе, нужно сложить все величины, а затем поделить их сумму на количество слагаемых. Мода – это рост, который имеет наибольшее число людей. Медиану вы получите, если выстроите всех людей по росту от самого низкого к самому высокому и возьмете рост человека, оказавшегося ровно посередине. В нормальном распределении среднее значение, мода и медиана равны. Такое распределение обладает и другими любопытными свойствами, и вскоре мы поговорим о них подробнее.

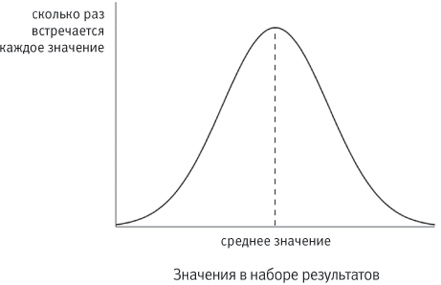
Нормальное распределение

Рост людей – лишь один пример величин, которые обычно приближаются к нормальному распределению. Таким же образом распределяются оценки на контрольных и показатели кровяного давления у населения. Как скажет вам любой актуарий и любой специалист по страхованию жизни, данные о продолжительности жизни людей тоже приближаются к нормальному распределению, пусть и немного асимметричному (выявляя эту асимметрию, они и зарабатывают деньги). Нормальное распределение повсюду. Хотя нам и неясно, как именно оно получило свое название, нормальное распределение вполне можно считать нормой распределения данных.

Как правило, нормальное распределение возникает, когда на измеряемый параметр одновременно незначительно влияет большое число независимых факторов (например, различные генетические, социальные и эволюционные факторы, определяющие, какой у человека будет рост), но существуют и другие формы распределения данных. Одну из них открыл Симеон Дени Пуассон.

Изучая число e в пятой главе, мы увидели, что распределения Пуассона наблюдаются тогда, когда события случаются редко, но при этом повторяются и остаются независимыми друг от друга. Пуассон изучал вероятность вынесения несправедливых приговоров в парижских судах в 1820-х годах, желая узнать, стали ли судьи лояльнее к гражданам (как выяснилось, не стали)[186]. Сегодня мы наблюдаем распределения Пуассона в различных системах, например, смотря на число голов в футбольных матчах (в Английской премьер-лиге чаще всего забивают по 2 и 3 гола) и на вероятное число метеоритов больше определенного размера, которые падают на Землю за год (для метеоритов диаметром более 22,4 метра в год с наибольшей вероятностью происходит 10, 11 или 12 столкновений).

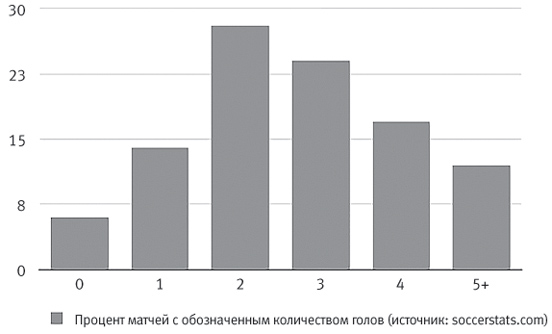
Пример распределения Пуассона: распределение голов в футбольных матчах Английской премьер-лиги в сезоне 2019–2020 годов

В каждом случае можно вычислить среднее и применить его к распределению Пуассона, чтобы сделать прогноз. Допустим, я управляю баром и знаю, что в среднем за вечер я продаю 10 ящиков пива. Как подготовиться к неожиданному наплыву клиентов? Покупать на всякий случай 20 ящиков нет смысла: это слишком затратно. Но если я куплю слишком мало ящиков – скажем, всего 12, – то возникнет риск, что пиво закончится и покажется, будто я не умею управлять баром. Новые клиенты никогда ко мне не вернутся.

Оказывается, я могу эмпирически оценить необходимое число ящиков на базе распределения Пуассона. Есть формула, которая дает мне вероятность того, что вечером потребуется x ящиков пива. В ней задействуется историческое среднее λ и (разумеется, как везде и всюду) число Эйлера e:

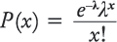
(Восклицательный знак после x обозначает “факториал”, то есть x умножается на x – 1, x – 2, x – 3 и так далее до единицы.)

Вероятность (P) того, что вечером понадобится 15 ящиков пива, составляет всего 3,5 %. Я продам 13 ящиков только в 7,3 % вечеров. 12 ящиков мне хватит в 9,5 % вечеров.

Какой же мне нужен запас? Если я могу себе такое позволить, то, пожалуй, 15 ящиков… Полностью распродавать их я буду (примерно) 12 раз за год. Но решать мне.

И это важно. По сути, статистика сводится к принятию субъективных решений. Это, если хотите, наука эмпирических предположений. Она напоминает математику и пахнет математикой, но в ней нет и следа той абсолютной уверенности, которую мы ассоциируем с этой наукой. Статистика говорит лишь о том, что вероятно при определенных числах и при определенных оценках достоверности чисел. Может, потому мы, попытавшись освоить математику, и испытываем трудности со статистикой.

С самого начала нашего путешествия мы видим, что человеческий мозг не слишком приспособлен для работы с числами. Статистика дается ему тяжелее всего. Мы смотрим на статистические данные и забываем об оговорках, которые их сопровождают. Или просто не можем понять, что именно они значат. Например, насторожитесь ли вы, если я скажу, что, по данным Всемирной организации здравоохранения, ежедневное употребление 50 граммов переработанного мяса – или бутерброда с двумя кусочками бекона – на 18 % повышает риск развития рака кишечника?[187]