Страх физики
Фейнмановские интегралы по траекториям представляют собой правила для расчёта квантово-механических процессов, и эти процессы в определённом смысле протекают именно таким способом. Представим себе все возможные пути, которыми частица может добраться из пункта А в пункт В:
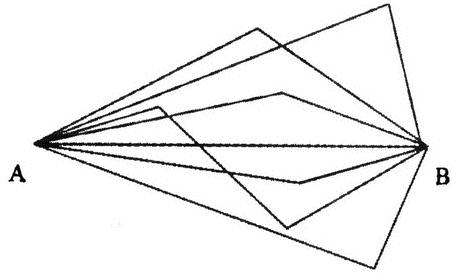
С каждым из путей связана некоторая вероятность того, что частица изберёт именно его. Самая сложная часть расчёта заключается в вычислении вероятности для каждого из путей и соответствующего этому пути мнимого времени, но мы этот технический момент опустим. Для макроскопических объектов, то есть таких, размеры которых во много раз превосходят размеры атомов, вероятность одного из возможных путей оказывается практически стопроцентной, в то время как вероятностями оставшихся путей можно пренебречь. Этот путь и является той траекторией, которую предсказывают законы классической механики. Но на расстояниях, сравнимых с размерами атомов, вероятности различных путей для частицы оказываются практически одинаковыми. В этом случае вероятность того, что частица, вылетев из пункта A, попадёт в пункт B, будет выражаться суммой вероятностей её прохождения по каждому из возможных путей.
Принципиальным отличием квантовой механики от классической является то, что вероятности в квантовой механике могут быть не только числами от 0 до 1, но и отрицательными числами, и даже мнимыми. Напомню, что мнимое число получается при извлечении квадратного корня из отрицательного числа. Если вам не нравятся мнимые вероятности, вы можете избавиться от них, представив мир, где мнимым может быть время. В этом случае вероятности будут записываться положительными числами. Мнимое время в данном случае — это не что-то загадочное, а просто математическая абстракция, использование которой облегчает квантово-механические расчёты. При вычислении окончательной вероятности попадания частицы из A в B после сложения всех вероятностей для всех возможных путей результат возводится в квадрат и, таким образом, всегда оказывается положительным действительным числом.
Важным моментом в этом расчёте является то, что мы всегда можем среди возможных путей найти два таких, вероятности которых при сложении взаимно уничтожатся, то есть дадут нулевой вклад в итоговую вероятность. Именно это имеет место при прохождении электрона через две щели. Давайте зафиксируем точку В на экране и закроем одну из щелей. В этом случае вероятность пути электрона из точки А в точку В будет ненулевой:
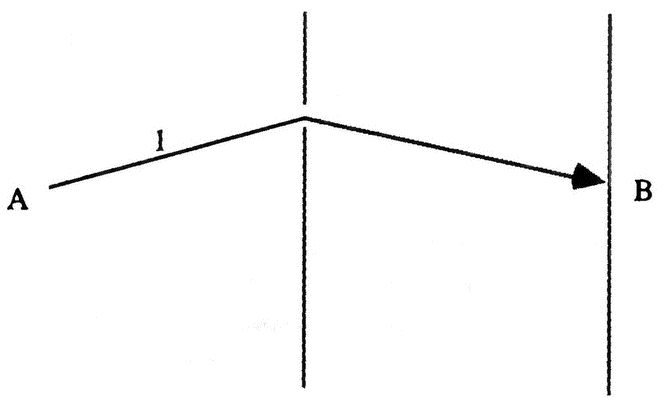
Точно так же мы получим ненулевую вероятность, если закроем другую щель:
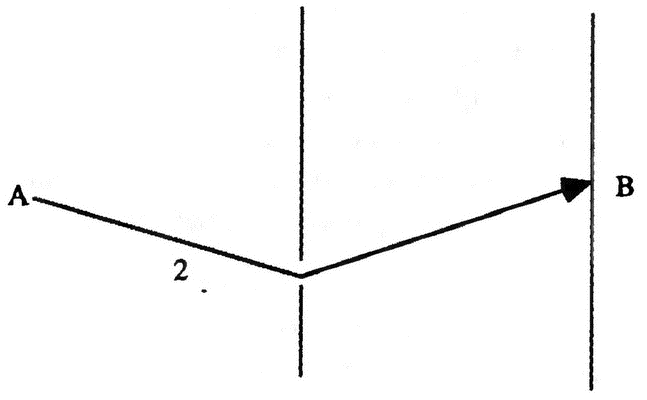
Но если мы откроем обе щели и сложим обе вероятности, то вполне может оказаться, что их сумма будет равна нулю:
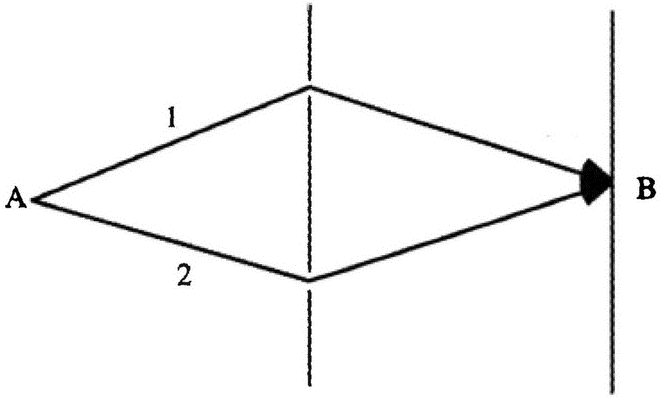
В реальном эксперименте это выглядит следующим образом: если мы оставляем открытой только одну из щелей, либо верхнюю, либо нижнюю, то наблюдаем в точке B вспышки от попадающих туда электронов. Если же мы открываем обе щели, то экран в точке B остаётся тёмным, даже если мы выпускаем электроны по одному. Электроны ведут себя так, как будто они и в самом деле проходят одновременно через обе щели! Если мы захотим узнать, как же на самом деле ведёт себя электрон, и поставим возле щелей детекторы, то они будут каждый раз фиксировать, что электрон пролетел либо через одну, либо через другую щель, а в точке B на экране будут фиксироваться вспышки — мы будем получать такие же результаты, как и в том случае, когда мы закрывали одну из щелей. Значит, установка детекторов каким-то образом изменяет правила расчёта вероятностей.
Я взял на себя труд описать всё это в деталях не столько для того, чтобы познакомить вас с явлением, имеющим основополагающее значение на атомных масштабах, сколько для того, чтобы показать, как этот невероятный, но подтверждённый опытным путём результат приводит при включении в рассмотрение специальной теории относительности к таким следствиям, с которыми было очень трудно смириться даже тем физикам, которые впервые их вывели. Но физика развивается именно путём проверки теорий на таких крайних случаях.
Если допустить, что электроны каким-то образом «исследуют» все доступные им траектории, а мы, в свою очередь, принципиально не можем узнать, что они делают на самом деле, то нам придётся смириться с тем, что утверждение о том, возможно или невозможно какое-либо из совершаемых электроном действий, имеет смысл в том и только в том случае, если мы имеем принципиальную возможность это действие наблюдать. Например, принцип неопределённости не позволяет нам точно определить несколько последовательных положений электрона, разделённых очень малыми промежутками времени, а это означает, что мы не можем определить «мгновенную» скорость электрона. Но тогда мы должны признать, что на очень коротких промежутках времени электрон может двигаться со сколь угодно большой скоростью, и даже быстрее света, что запрещено специальной теорией относительности.
Таким образом, мы приходим к известному философскому вопросу: «Издаёт ли звук падающее дерево, если рядом нет никого, кто мог бы этот звук услышать?» Или в нашем случае: «Может ли частица в течение очень коротких промежутков времени превышать скорость света, если мы принципиально не можем обнаружить этот факт из-за принципа неопределённости, и более того, если этот факт вообще не имеет никаких наблюдаемых последствий?» В обоих случаях ответ: «Да».
Специальная теория относительности настолько тесно связывает пространство и время, что накладывает ограничение на максимальную скорость, которая определяется как отношение пройденного расстояния к промежутку времени, за которое оно пройдено. Одним из следствий такой связи является то, что тело, движущееся быстрее света, должно при этом двигаться вспять во времени! Это одна из причин запрета подобных движений, в противном случае возникнет нарушение причинно-следственных связей, которое так любят эксплуатировать писатели-фантасты, например отправляя героя в прошлое, где он убивает свою бабушку, делая невозможным собственное рождение. Но квантовая механика не запрещает частицам в течение очень коротких промежутков времени двигаться быстрее света при условии, что такое движение в силу принципа неопределённости никаким способом не может быть обнаружено. До тех пор пока мы принципиально не можем измерить сверхсветовую скорость частицы, она не нарушает никаких требований специальной теории относительности. Но чтобы квантовая теория оставалась согласованной со специальной теорией относительности, в течение таких интервалов времени частица, двигаясь со сверхсветовой скоростью, должна путешествовать назад во времени.
Что это означает на практике? Нарисуем траекторию электрона, как бы она выглядела с точки зрения гипотетического наблюдателя, способного фиксировать мгновенные прыжки во времени:
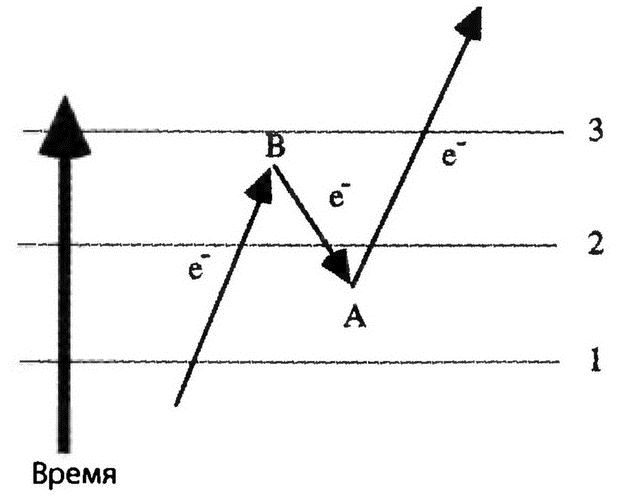
Этот наблюдатель обнаружит в момент времени 1 одну частицу, в момент времени 2 — три частицы и в момент времени 3 — снова одну частицу. Другими словами, количество частиц, наблюдаемых в каждый момент времени, для такого наблюдателя не сохраняется! В один момент времени он видит один электрон, а в другой у электрона вдруг появляется пара попутчиков, причём один из этих попутчиков движется вспять во времени.
Но как должен выглядеть электрон, который движется вспять во времени? Мы делаем вывод о том, что наблюдаемая частица является электроном, измеряя её массу и электрический заряд. А как мы измеряем заряд частицы? Обычно на основании того, в какую сторону отклоняется частица в электрическом или магнитном поле. Допустим, электрон, заряженный отрицательно, отклоняется вправо. Если электрон движется вспять во времени, то наблюдатель, для которого время по-прежнему движется вперёд, будет наблюдать полёт этого электрона, как в запущенном в обратную сторону кинофильме, то есть он увидит частицу, которая по отношению к направлению своего движения будет отклоняться влево, как если бы эта частица имела не отрицательный, а положительный заряд. Теперь мы можем описать, что увидит наблюдатель в показанном на предыдущем рисунке случае:

С этой точки зрения картина выглядит уже не такой странной. В некоторый момент времени в точке А появляются из ниоткуда две частицы, одна из которых, так же как и электрон, заряжена отрицательно, а вторая — положительно. Положительная частица движется навстречу первому электрону и встречается с ним в точке B, где они взаимно уничтожаются, а второй электрон продолжает своё путешествие.
Как я уже говорил, никакой реальный наблюдатель не способен измерить скорость электрона между моментами времени 1 и 3 — это запрещает принцип неопределённости. Точно так же никакой реальный наблюдатель не способен обнаружить рождение частиц из ничего, равно как и измерить скорость частицы, движущейся быстрее света. Но независимо от того, можем мы или нет зарегистрировать такие процессы, квантовая механика их не запрещает. Если рождение и уничтожение частиц происходит на таких временных интервалах, когда принцип неопределённости делает невозможным их обнаружение, то никаких противоречий со специальной теорией относительности не возникает. Такие частицы называются
Уравнение, объединяющее квантовую механику и специальную теорию относительности применительно к электронам, было впервые выведено в 1928 году британским физиком Полем Адриеном Морисом Дираком, одним из отцов-основателей квантовой механики, занимавшим с 1932 по 1969 год пост Лукасовского профессора математики (в своё время этот пост занимал Исаак Ньютон, а с 1979 по 2009 год — Стивен Хокинг). Теория, объединившая квантовую механику и специальную теорию относительности, получила название
Никакие два других физика не были столь различны меж собой, как Дирак и Фейнман. Фейнман был экстравертом, Дирак — интровертом. Отец Дирака, будучи родом из Швейцарии, преподавал в Бристоле французский язык и требовал от своего среднего сына Поля говорить дома только по-французски. Будучи не в состоянии точно и полно выражать свои мысли на французском, Поль предпочитал молчать, и эта молчаливость осталась с ним на всю жизнь.
Рассказывают, и это похоже на правду, что Нильс Бор — директор института в Копенгагене, куда поступил на работу Дирак после получения докторской степени в Кембридже, — вскоре после знакомства с Дираком посетил Эрнеста Резерфорда. Бор пожаловался Резерфорду на то, что поступивший к нему на работу молодой физик за всё это время не произнёс ни одного слова. В ответ Резерфорд рассказал Бору анекдот: «Стеснённый в средствах покупатель заходит в магазин, чтобы приобрести попугая. Хозяин предлагает ему первого попугая красивой жёлто-белой расцветки, знающего 300 слов. Цена птицы — $5000. Покупатель отказывается, тогда хозяин предлагает ему другого попугая, ещё более красивого и говорящего на четырёх языках, — за $25 000. Покупатель, обескураженный ценой, оглядывается по сторонам и обращает внимание на невзрачного попугая, сидящего на жёрдочке в дальнем углу магазина. На вопрос, сколько стоит эта птица, следует ответ: $100 000. „Сколько же иностранных языков знает этот попугай“, — потрясённо спрашивает покупатель. „Ни одного, — отвечает продавец, — он вообще не разговаривает!“ — „Но почему же тогда он стоит так дорого?“ — „Потому что он думает!“»
Как бы то ни было, Дирак не питал склонности к визуализации в физике. Напротив, он наиболее комфортно чувствовал себя среди уравнений и после нескольких лет работы наконец вывел замечательное уравнение, корректно описывающее релятивистское поведение электрона. Спустя какое-то время стало понятно, что это уравнение предсказывает существование частицы, эквивалентной электрону, но имеющей положительный заряд, причём она может существовать не только как виртуальная пара виртуального же электрона, но и как самостоятельная, вполне реальная наблюдаемая частица.