Теорема века. Мир с точки зрения математики

Пусть читатель будет спокоен; чтобы понять рассуждение, которое последует, ему нет необходимости знать, что такое порядковое трансфинитное число.

Между тем Кантор точно показал, что между двумя трансфинитными числами, как и между двумя конечными числами, не может быть другого отношения, кроме равенства либо неравенства в ту или другую сторону. Но не о сути этого мемуара хочу я здесь говорить, это увлекло бы меня далеко от моего предмета. Я хочу лишь заняться формой и задаюсь вопросом, много ли выиграл автор в строгости положений, применяя эту форму, и вознаграждает ли она за те усилия, которые писатель и читатель должны употребить.

Мы видим, что Бурали-Форти определяет число 1 следующим образом:

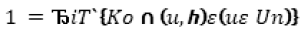
Это определение в высшей степени подходит для того, чтобы дать представление о числе 1 тем лицам, которые никогда о нем ничего не слышали!

Я слишком мало понимаю приверженцев Пеано, чтобы рискнуть его критиковать; но я опасаюсь, что это определение заключает petitio principii, так как я вижу цифру 1 в первой части и изображенное буквами слово «один» (Un) во второй части равенства.

Как бы то ни было, Бурали-Форти исходит из этого определения и после коротких вычислений приходит к уравнению

1εNO,

которое дает нам понять, что «один» есть число.

Так как нам теперь приходится иметь дело с определениями простых чисел, то мы напомним, что Кутюра также определил 0 и 1.

Что такое нуль? Это число элементов нулевого класса. А что такое нулевой класс? Это класс, который не содержит никакого элемента.

Определять нуль при помощи нулевого класса, а нулевой класс при помощи термина «никакой» – это значит поистине злоупотреблять богатством языка; поэтому Кутюра ввел усовершенствование в свое определение, написав:

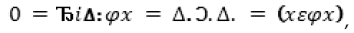
что обозначает: нуль есть число предметов, удовлетворяющих такому условию, которое никогда не выполняется.

Но так как «никогда» обозначает «ни в одном случае», то я не вижу значительного успеха в этой замене.

Спешу прибавить, что определение, которое Кутюра дает числу 1, более удовлетворительно.

«Один, – говорит он, – в сущности, есть число элементов класса, два любых элемента коего тождественны».

Это определение более удовлетворительно, как я сказал, в том смысле, что для определения понятия 1 автор не пользуется словом «один». Но зато он пользуется словом «два». И я боюсь, что если спросить у Кутюра, что такое «два», то он должен будет в ответе воспользоваться словом «один».

VIII

Вернемся к мемуару Бурали-Форти. Я сказал, что его заключения прямо противоположны выводам Кантора. Но однажды меня посетил Адамар. Разговор коснулся этой антиномии.

– Не кажется ли вам, – сказал я, – что рассуждение Бурали-Форти безупречно?

– Нет, напротив, я не вижу в нем никаких возражений Кантору. Кроме того, Бурали-Форти не имел права говорить о совокупности всех порядковых чисел.

– Простите, он имел это право, потому что всегда мог написать: