Страх физики

Ещё важнее то, что упомянутая величина s является в теории относительности аналогом длины линейки L из предыдущего примера. Эта мера — s — называется пространственно-временным интервалом и определяется как s² = с²t² — d². Она представляет собой комбинацию пространственного и временного интервалов между событиями и всегда равна нулю для двух событий, лежащих на пространственно-временной траектории луча света. То есть если свет, испущенный из точки, в которой происходит первое событие, достигает точки, в которой происходит второе событие в момент этого события, то пространственно-временной интервал между этими событиями равен нулю. Интервал одинаков для всех наблюдателей, независимо от того, как они движутся друг относительно друга. Если два события не лежат на пространственно-временной траектории луча света, то интервал между ними будет отличен от нуля, но он по-прежнему будет одним и тем же для всех наблюдателей.

Таким образом, интервал s является, как говорят, инвариантом в теории относительности. Интервал для движущихся по-разному наблюдателей представляет собой то же, что длина линейки для пещерных обитателей. В теории относительности интервал — это пространственно-временная длина. Три пространственных измерения и время оказываются тесно связанными друг с другом, наподобие того, как тесно связаны две проекции линейки на стенах пещеры. Движение объекта приводит к изменению проекции четырёхмерного пространства-времени на трёхмерную сцену, которую мы называем словом «сейчас», подобно тому как поворот линейки приводит к изменению её двухмерной проекции на стену пещеры! Эйнштейн, руководствуясь постулатом о постоянстве скорости света, получил возможность сделать то, о чём большинство из нас могло бы только мечтать. Он выглянул за стены пещеры и увидел доселе скрытую от него реальность, подобно тому как наш персонаж однажды обнаружил, что круглая и прямоугольная тени на стене пещеры принадлежат цилиндрическому контейнеру. Но к чести Эйнштейна, он на этом не остановился. Картина ещё не была завершена. Его путеводной нитью снова оказался луч света. Все наблюдатели, движущиеся с постоянной скоростью, видят луч света, движущийся относительно них со скоростью c, и ни один из них не может утверждать, что он покоится, в то время как движутся все остальные. Движение относительно. Но что, если скорость движения наблюдателей не постоянна! Что, если один из них движется с ускорением? Смогут ли в этом случае все наблюдатели, включая ускоряющегося, однозначно утверждать, что один из них движется с ускорением? Чтобы исследовать этот вопрос, Эйнштейн придумал ещё один мысленный эксперимент. Как вы определяете, находясь в лифте, когда и в каком направлении он начинает движение? Когда лифт начинает движение вверх, вы чувствуете, что стали немного тяжелее; когда же лифт начинает двигаться вниз, вы ощущаете, что стали легче. Но откуда вы знаете, что изменение вашего веса вызвано ускорением лифта, а не изменением силы тяжести?

Не спешите с ответом. Не существует ни одного эксперимента, который дал бы запертому в лифте наблюдателю ответ, движется лифт с ускорением или покоится в гравитационном поле. Давайте упростим мысленный эксперимент. Пусть лифт находится в глубоком космосе вдали от тяготеющих тел. Когда он находится в состоянии покоя или движется равномерно и прямолинейно, мы испытываем внутри него полную невесомость. Если лифт начнёт ускоряться, скажем, вверх, его пол начнёт давить на ноги, чтобы придать вам такое же ускорение, которое испытывает он сам. Если вы выпустите мяч из ваших рук, он начнёт «падать» на пол. Почему? Потому что если мяч первоначально находился в состоянии покоя, то он, согласно Галилею, будет стремиться сохранить это состояние, однако пол лифта движется вверх с ускорением и в конце концов настигнет мяч. С вашей точки зрения, это будет выглядеть, как будто мяч с ускорением полетел вниз и ударился об пол. Более того, ускорение мяча не зависит от его массы. Действительно, какой бы мяч вы ни взяли, пол лифта настигнет его через тот же самый промежуток времени.

Если бы Галилей оказался вместе с вами в лифте, он мог бы поклясться, что находится на Земле. Все опыты с падающими телами, которые он поставил за свою жизнь, будут проходить в таком лифте точно так же, как и на поверхности Земли. Таким образом, если Галилей пришёл к выводу, что все законы физики выполняются одинаково во всех системах отсчёта, движущихся равномерно и прямолинейно, то Эйнштейн пошёл дальше и понял, что законы физики должны быть одинаковы для системы отсчёта, движущейся с постоянным ускорением, и для системы отсчёта, покоящейся в гравитационном поле. С этой точки зрения ускорение тоже относительно, просто один наблюдатель назовёт его ускорением, а другой — гравитацией.

Снова Эйнштейн выглянул за пределы пещеры. Если гравитация может быть «создана» внутри лифта, то, может быть, мы все живём внутри метафорического лифта? Может быть, то, что мы называем гравитацией, на самом деле является ускорением, и всё зависит только от выбранной точки зрения? Мы живём на Земле. Земля обладает большой массой. Возможно, то, что мы воспринимаем как силу притяжения между двумя массами, является результатом какого-нибудь хитрого искажения окружающего нас пространства-времени?

Чтобы сложить получившийся пазл, Эйнштейн снова обратился к свету. Он показал, что постоянство скорости света должно определять способ, которым пространство и время сшиваются вместе. Что делает луч света в ускоряющемся лифте? Для внешнего наблюдателя свет будет распространяться с постоянной скоростью по прямой линии. Но для наблюдателя, находящегося внутри ускоряющегося лифта, траектория луча света окажется искривлённой:

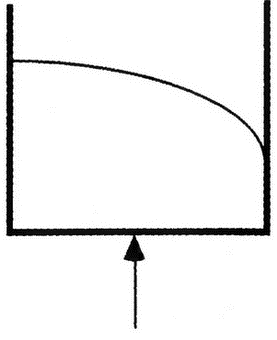
В системе отсчёта лифта луч света будет отклоняться вниз, потому что лифт ускоряется вверх. Другими словами, свет будет «падать». Но если ускорение в лифте эквивалентно покою в гравитационном поле, то луч света должен изгибаться, проходя мимо массивных тел. По большому счёту, это неудивительно. Эйнштейн к тому времени уже показал, что масса и энергия эквивалентны и взаимозаменяемы. Энергия светового луча увеличивает массу поглощающего его тела. Аналогично масса тела может перейти в излучение и быть унесённой лучом света в виде энергии. Таким образом, если свет может нести энергию, то он может вести себя так, будто он имеет массу, а все массивные объекты попадают в гравитационное поле.

Но с этим понятием имеется одна фундаментальная проблема. Падающий мяч ускоряется. Его скорость зависит от его координат. Однако мы же только что подвели постоянство скорости света под фундамент специальной теории относительности. Свет всегда должен путешествовать с одной и той же скоростью, независимо от того, как движется наблюдатель по отношению к лучу света и по отношению к другим наблюдателям. Поэтому наблюдатель, располагающийся в левой верхней части лифта, должен при измерении скорости света получить значение c. Но наблюдатель в правой нижней части лифта должен получить то же самое значение c, несмотря на то что к моменту, когда свет дошёл до него, его скорость успела возрасти по сравнению со скоростью первого наблюдателя.

Как примирить эти результаты с выводом, что луч света в лифте изгибается, потому что он «падает»? Кроме того, поскольку Эйнштейн постулировал, что в гравитационном поле должны иметь место те же явления, что и в ускоряющемся лифте, свет в гравитационном поле тоже должен «падать». Это может произойти, только если скорость света будет разной в разных точках пространства!

Есть только один способ примирить два противоречащих друг другу поведения света: искривление светового луча под действием гравитационного поля или внутри ускоряющегося лифта и постоянство скорости света для любого наблюдателя: масштаб линеек и ход часов различных наблюдателей, даже находящихся в одной системе отсчёта — в ускоряющемся лифте или на поверхности Земли, — должны зависеть от их положения в пространстве и времени!

Что в этом случае происходит с пространством и временем? Чтобы понять это, вернёмся снова в нашу пещеру. Предположим, что на плоской стене пещеры изображена карта, на которую нанесён путь самолёта, следующего из Нью-Йорка в Бомбей:

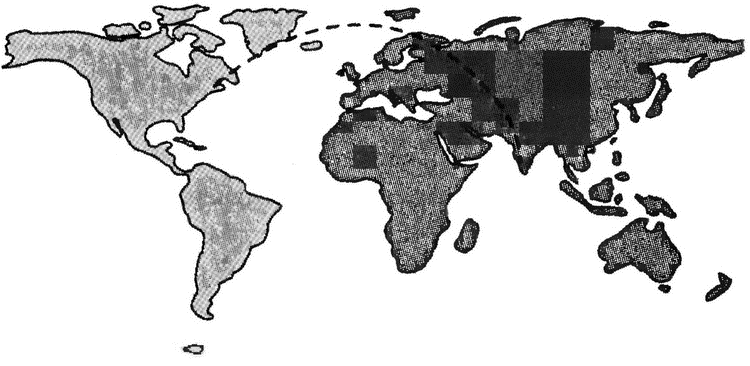
Можем ли мы добиться того, чтобы кривая траектория на этом рисунке выглядела локально как прямая линия, вдоль которой самолёт двигался бы равномерно и прямолинейно? Один из способов — позволить линейкам изменять свою длину в зависимости от широты места. Как вы, возможно, заметили, Гренландия на этой карте выглядит больше Европы. Если линейка в полярных широтах имеет большую длину, чем в средних, то географ, отправившись с этой линейкой в Гренландию и измерив её размеры, что называется, «на месте», а затем проделав то же самое в Европе, убедится, что при подобных локальных измерениях Гренландия оказывается гораздо меньше Европы.

Для обитателя пещеры такое предложение может показаться безумным, но не для нас, знающих, что Земля круглая. Предложенное решение эквивалентно предположению, что поверхность, на которой изображена карта, на самом деле неплоская, а приведённое изображение представляет собой проекцию на плоскость стены пещеры карты, нарисованной на сфере. И на реальной земной сферической поверхности расстояния при приближении к полюсам действительно сокращаются по сравнению с изображёнными на плоской карте. Если перенести траекторию самолёта на глобус, то сразу же станет очевидно, что она представляет собой кратчайший путь из Нью-Йорка в Бомбей, и самолёт действительно будет двигаться вдоль неё с постоянной скоростью и не меняя направления.

Какой из этого следует вывод? Если мы хотим быть последовательными, мы должны признать, что для разрешения упомянутого ранее противоречия пространство-время в системе отсчёта, движущейся с ускорением или находящейся в гравитационном поле, должно быть искривлённым. Почему же мы не ощущаем эту кривизну, если она на самом деле существует? Потому что мы всегда воспринимаем пространство локально в небольшой окрестности. Представьте себе таракана, живущего в Канзасе. Мир для него представляет собой плоскую, как доска, двухмерную поверхность. Только позволив себе роскошь посмотреть на эту поверхность из трёхмерного пространства, можно увидеть, что на самом деле она представляет собой поверхность сферы. Аналогично, чтобы увидеть кривизну трёхмерного пространства, надо посмотреть на него из четырёхмерного, но это так же невозможно для нас, как невозможно для таракана, обречённого вечно ползать по поверхности земли, — трёхмерное пространство находится за пределами его восприятия.

В этом смысле Эйнштейн был Эратосфеном XX века. Эратосфен утверждал, что Земля — шар, и чтобы в этом убедиться, достаточно пронаблюдать за тем, на какую высоту поднимается в полдень солнце в разных городах[16]. Эйнштейн утверждал, что трёхмерное пространство искривлено, и чтобы в этом убедиться, достаточно пронаблюдать за поведением светового луча в гравитационном поле. Эйнштейн предложил три способа проверки его гипотезы.

Во-первых, при прохождении через искривлённое пространство рядом с Солнцем световой луч должен отклоняться на вдвое больший угол, чем если бы он просто падал в плоском пространстве. Во-вторых, если пространство возле Солнца искривлено, то орбита ближайшей к Солнцу планеты Меркурий должна представлять собой не идеальный эллипс, а рисовать в пространстве «розетку», что должно приводить к медленному смещению перигелия — наиболее близкой к Солнцу точки орбиты. И в-третьих, часы на первом этаже небоскрёба должны идти медленнее, чем на последнем.

Смещение перигелия Меркурия было известно уже давно, и расчёт Эйнштейна прекрасно совпал с наблюдаемой величиной. Однако объяснение чего-то уже известного не так впечатляет, как предсказание чего-то нового. Два других предсказания Эйнштейна относились как раз к последней категории.

В 1919 году экспедиция под руководством сэра Артура Стэнли Эддингтона отправилась в Южную Африку для наблюдения полного солнечного затмения. Когда луна закрыла солнечный диск, Эддингтон сфотографировал звёзды, расположенные вблизи Солнца. Сравнив полученную фотографию с фотографией, выполненной в другое время года, он определил, что видимые положения звёзд во время затмения отличаются от обычных в точности на предсказанную Эйнштейном величину. Луч света действительно изгибался, проходя мимо Солнца, а имя Эйнштейна с тех пор стало нарицательным.

Третья проверка была выполнена лишь сорок лет спустя. Сотрудник Гарвардского университета Роберт Паунд и его аспирант Глен Ребка показали, что частота света, излучённого в подвале физической лаборатории, уменьшается, когда свет достигает приёмника, расположенного на верхнем этаже. И это изменение частоты точно совпало с предсказанным Эйнштейном.

С точки зрения общей теории относительности искривление траектории и ускорение движущегося в гравитационном поле тела могу быть представлены как проявление кривизны пространства. Чтобы это понять, вернёмся снова к двухмерной аналогии. Представим себе, что мы видим на стене пещеры следующую проекцию траектории движения тела вокруг большого объекта.