Страх физики

Для объяснения такого движения можно придумать силу, которая действует на небольшое тело со стороны большого. Но можно предположить, что настоящая поверхность, по которой движется тело, искривлена в трёхмерном пространстве, и тело движется со своей точки зрения «прямо», но его траектория проходит по искривлённой поверхности:

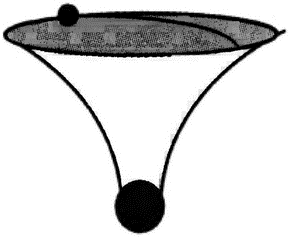
Похожие аргументы использовал и Эйнштейн, утверждая, что вместо силы притяжения, действующей между двумя телами, можно рассматривать ситуацию, когда массивное тело искривляет пространство-время вокруг себя, а другие тела, стремясь двигаться «прямо» в искривлённом пространстве — времени, движутся по искривлённым траекториям. Это замечательное соотношение между материей и пространством-временем напоминает Уробороса — змея, который кусает себя за хвост. Кривизна пространства управляет движением материи, распределение материи в пространстве, в свою очередь, управляет кривизной пространства. Именно эта обратная связь между материей и кривизной делает общую теорию относительности намного сложнее ньютоновской механики, где пространство, в котором перемещаются объекты, абсолютно и неизменно.

В привычном окружающем нас мире кривизна пространства настолько мала, что её последствия практически незаметны, и это является одной из причин, по которой понятие искривлённого пространства кажется нам чуждым. Путешествуя из Нью-Йорка в Лос-Анджелес, луч света отклоняется из-за искривления пространства, вызываемого массой Земли, всего на один миллиметр. Однако если время путешествия света велико, то даже небольшой эффект может привести к заметным последствиям. Возьмём, к примеру, сверхновую 1987 года, о которой я уже упоминал как об одном из самых интересных астрономических событий XX века. Нетрудно посчитать — и мы с моим коллегой действительно подсчитали и поразились настолько, что написали об этом научную статью, — что небольшой кривизны пространства, сквозь которое свет от сверхновой 1987 года добирается до нас с другого конца Галактики, оказалось достаточно, чтобы задержать его прибытие на девять месяцев! Если бы пространство не было искривлено, мы увидели бы вспышку сверхновой 1987 года ещё летом 1986-го.

Финальным испытательным полигоном для идей Эйнштейна стала сама Вселенная. Общая теория относительности описывает не только искривление пространства вблизи массивных тел, но и геометрию всей Вселенной. Если средняя плотность вещества во Вселенной окажется достаточно большой, то пространство может искривиться настолько, что замкнётся в гигантский аналог сферы в трёхмерном пространстве. Но что ещё более важно, в этом случае Вселенной придётся рано или поздно остановить своё расширение и начать сжиматься, придя в конечном итоге к Большому сжатию — явлению, обратному Большому взрыву.

Есть что-то зачаровывающее в «закрытой» Вселенной — как называют Вселенную с высокой средней плотностью вещества. Я помню, как, будучи ещё студентом, впервые услышал об этом на лекции астрофизика Томаса Голда и запомнил на всю жизнь. В закрытой Вселенной, которая замкнута сама на себя, луч света, движущийся по прямой линии, в конечном итоге вернётся в ту точку, из которой он вышел, подобно тому как вернётся в исходную точку путешественник, совершивший кругосветное путешествие на поверхности Земли. То есть свет в такой Вселенной никогда не сможет уйти в бесконечность. Когда подобное происходит в меньших масштабах, то есть когда космический объект имеет настолько высокую плотность, что даже свет не может убежать с его поверхности, мы называем его чёрной дырой.

Если наша Вселенная закрыта, то мы сами живём внутри самой настоящей чёрной дыры! Но не в той, которая показана в диснеевском фильме 1979 года. Суть в том, что чем больше размер чёрной дыры, тем меньше должна быть плотность вещества, необходимая для её создания. Чёрная дыра с массой Солнца будет иметь размер порядка километра и среднюю плотность в сотни миллиардов тонн на кубический сантиметр. Чёрная дыра с массой, равной массе наблюдаемой части Вселенной, будет иметь размер, сравнимый с размером видимой части Вселенной, при средней плотности всего лишь порядка 10^-29 грамма на кубический сантиметр!

Сегодняшние наблюдательные данные, однако, свидетельствуют о том, что мы живём не внутри чёрной дыры. По крайней мере, большинство теоретиков считает, что средняя плотность вещества во Вселенной хотя и близка к критической, но всё же недостаточна, чтобы закрыть Вселенную. По данным наблюдений, наш мир, скорее всего, избежит Большого сжатия и будет продолжать расширяться вечно. Характер расширения Вселенной более всего соответствует пограничному случаю между открытой и закрытой Вселенными, который носит название плоской Вселенной, и если источником гравитационного притяжения служит материя, то расширение Вселенной будет в этом случае происходить замедляющимися темпами, но никогда не остановится. Так как для плоской Вселенной необходима средняя плотность вещества примерно в 100 раз больше наблюдаемой, теоретики пришли к выводу, что на 99% Вселенная состоит из тёмной материи, невидимой для телескопов, о чём я уже рассказывал в главе 3. Причём даже рассчитанного путём «взвешивания» галактик и скоплений галактик количества тёмного вещества всё равно оказывается в три раза меньше, чем необходимо для плоской Вселенной.

Как мы можем доказать правильность этого предположения? Например, можно попытаться определить среднюю плотность в галактиках и скоплениях галактик, как описывалось в главе 3, но это косвенный способ, который не даёт прямых свидетельств плоскости Вселенной. Однако существует способ, позволяющий — по крайней мере, в принципе — напрямую измерить кривизну пространства. Каким образом разумный таракан из Канзаса мог бы удостовериться в кривизне земной поверхности, не совершая кругосветного путешествия и не поднимаясь в космос? Даже не будучи в состоянии представить себе сферу в трёхмерном пространстве, подобно тому как мы не можем представить себе трёхмерную гиперсферу в четырёхмерном пространстве, он мог бы провести ряд измерений, которые убедили бы его в том, что поверхность Земли является сферой. Ещё Евклид более двадцати веков назад доказал, что сумма трёх углов в любом треугольнике, начерченном на бумаге, равна 180°. Если я нарисую прямоугольный треугольник, один из углов которого имеет величину 90°, сумма двух других углов также должна составлять 90°. Поэтому каждый из оставшихся углов должен быть меньше 90°, как показано на следующем рисунке:

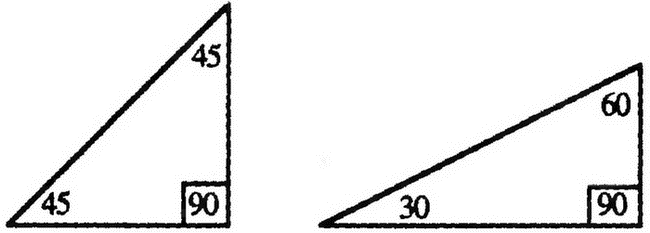
Но это справедливо только на плоскости. На поверхности сферы я могу нарисовать треугольник, все углы которого будут иметь величину 90°. Для этого достаточно провести одну линию по экватору от нулевого до девяностого меридиана, а от её концов провести две линии, пересекающиеся на Северном полюсе:

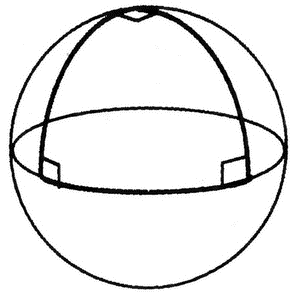
Если вы помните, окружность радиуса r имеет длину 2πr. Однако на сфере длина любой параллели всегда меньше, чем умноженное на 2π расстояние от полюса до этой параллели, отмеренное по поверхности сферы. Данная ситуация показана на следующем рисунке:

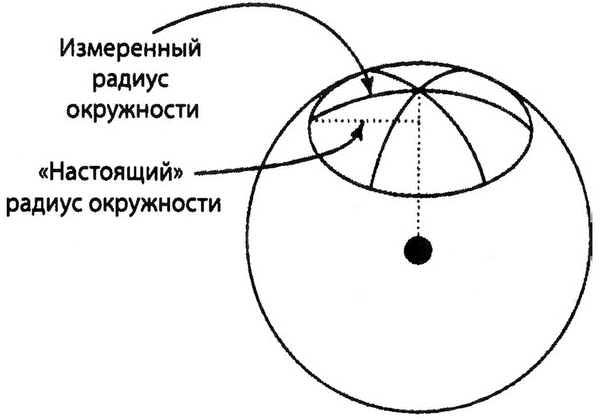
Нарисовав на поверхности Земли большой треугольник или большую окружность, мы по отклонению от предсказаний Евклида можем вычислить кривизну земной поверхности и определить, что она является сферой. Однако, как видно из рисунка, для того чтобы получить существенное отклонение от геометрии Евклида, нужно нарисовать очень большие геометрические фигуры, сравнимые с размерами Земли.

Для того чтобы произвести аналогичные измерения во Вселенной, нам нужно выполнить геометрические построения, размеры которых сравнимы с размерами самой Вселенной. Вместо окружности мы можем взять сферу в трёхмерном пространстве и попытаться определить, как изменяются площадь её поверхности и объём ограничиваемого ею шара с увеличением радиуса. Если измерения разойдутся с предсказаниями Евклида, значит, пространство нашей Вселенной искривлено.

Но как измерить объём сферы, размер которой составляет существенную часть видимой Вселенной? Ну, например, подсчитав число галактик, находящихся внутри этой сферы, предположив, что Вселенная однородна и плотность галактик в каждый момент времени одинакова в любой части Вселенной. В этом случае мы могли бы считать, что объём сферы пропорционален количеству находящихся внутри неё галактик, и всё, что нам останется, это построить график зависимости числа наблюдаемых галактик от расстояния до них. Если пространство искривлено, мы должны увидеть отклонение этого графика от предсказываемого евклидовой геометрией. В 1986 году два молодых принстонских астронома Е. Лох и Е. Спиллар произвели такой подсчёт, и полученный ими результат якобы свидетельствовал в пользу того, что Вселенная является плоской. К сожалению, вскоре после публикации их работы было показано, что галактики, эволюционируя, могут сливаться друг с другом, и на основании подсчёта их количества нельзя сказать о характере геометрии нашей Вселенной ничего определённого.

Ещё одним способом проверить геометрию Вселенной является измерение зависимости угла, под которым виден объект известного размера, от расстояния до этого объекта. На плоскости угол, под которым виден объект, будет уменьшаться с ростом расстояния:

Однако на сфере картина будет совсем иной:

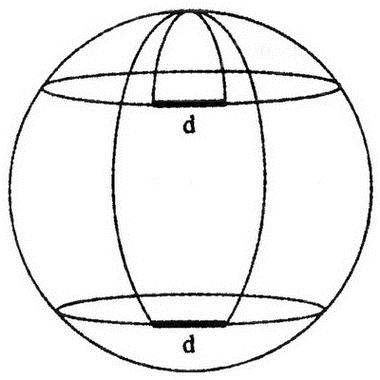
В начале 1990-х годов было предпринято исследование зависимости угла, под которым видны очень компактные объекты в центрах галактик, от расстояния до них. Измерения производились при помощи радиотелескопов, и в обзор попали галактики, находящиеся от нас на расстояниях вплоть до половины радиуса наблюдаемой Вселенной. Полученная зависимость снова свидетельствовала в пользу того, что пространство нашей Вселенной плоское. Однако мы с коллегой показали, что и этот тест содержит неопределённость, связанную с возможной эволюцией исследуемых объектов.

В 1998 году неожиданно появилась совершенно новая возможность определения геометрии Вселенной на основе измерений неоднородности фона космического микроволнового излучения, называемого также реликтовым излучением, являющегося отголоском Большого взрыва.

Реликтовое излучение, впервые открытое в 1965 году, приходит к нам со всех сторон. Оно возникло почти 14 миллиардов лет назад и последний раз эффективно взаимодействовало с веществом, когда Вселенной было всего лишь 100 000 лет от роду. В ту давнюю эпоху это излучение имело температуру примерно 3000 градусов по абсолютной шкале Кельвина. В результате сегодня это излучение даёт нам картину распределения материи и излучения в ранней Вселенной. Так как излучение, которое мы видим сегодня, приходит равномерно со всех сторон, оно «рисует» для нас сферическую поверхность, существовавшую почти 14 миллиардов лет назад, когда это излучение в последний раз провзаимодействовало с веществом.

Эта сферическая поверхность предоставляет нам идеальную возможность использовать уже описанный ранее геометрический метод, если найти какой-нибудь эталон длины на этой сфере, угловой размер которого мы могли бы затем измерить. К счастью, природа предоставила именно такой эталон. Поскольку сила гравитации — это всегда сила притяжения, то любой фрагмент вещества всегда стремится сжаться под действием собственной гравитации, если только его не удерживает от этого какая-то дополнительная сила. Прежде чем Вселенная остыла до температуры ниже 3000 Кельвин, вещество состояло главным образом из сильно ионизированного водорода, который интенсивно взаимодействовал с излучением, оказывающим давление на вещество. Это давление предотвращало сжатие любого фрагмента вещества, если размеры этого фрагмента не превосходили некоторое критическое значение.

Вы спросите, что это за критическое значение? Сейчас объясню. Когда Вселенной было всего 100 000 лет, свет мог путешествовать по ней на расстояние не более 100 000 световых лет. Поскольку ничто не может распространяться быстрее света, то и гравитационное взаимодействие могло осуществляться только между телами, расстояние между которыми не превышало 100 000 световых лет. Это значит, что в это время максимальный размер неоднородностей вещества не мог превышать 100 000 световых лет. Когда же Вселенная остыла до 3000 Кельвин, водород рекомбинировал и перестал взаимодействовать с излучением. Давление излучения упало практически до нуля, и первоначальные неоднородности начали сжиматься под действием собственной гравитации. И первоначальный размер этих неоднородностей оказался как раз порядка 100 000 световых лет.