Искусство большего. Как математика создала цивилизацию

Это, пожалуй, вполне правдоподобно. Но дальше Бартлетт спрашивает, насколько полной бутылка окажется в 11:56, всего за 4 минуты до конца эксперимента? Математика показывает, что бутылка будет заполнена всего на 6 %. Это не очевидно: будь вы бактерией в бутылке, вам бы в этот момент не показалось, что место скоро закончится. Даже за 2 минуты до конца эксперимента бутылка полна всего на четверть. Она полна наполовину за 1 минуту до полудня. И после этого при последнем удвоении (происходящем в последнюю минуту) она наполняется по самое горлышко.

Еще удивительнее то, что произойдет, если Бартлетт в 11:58 даст вам три новые бутылки, когда первая заполнится лишь на четверть. Бутылка у вас в руке почти пуста, а на полке стоят еще три. Похоже, они заполнятся еще нескоро. Но это не так. Вторая бутылка заполнится в 12:01. Уже в 12:02 полны окажутся все четыре бутылки.

По прошествии 58 минут бактериального деления вы с оптимизмом смотрели в будущее. Еще через четыре минуты от вашего оптимизма не осталось и следа. В этом, по словам Бартлетта, и заключается трагедия нашего непонимания экспонент – хоть в применении к распространению болезней, хоть при бесконтрольном росте численности населения. В начале лекции он неизменно отмечал: “Величайший недостаток человечества – его неспособность понять экспоненциальную функцию”.

У этого недостатка есть название. Это недооценка экспоненциального роста, которая встречается не только в мире эпидемий и увеличения численности населения. В научной литературе речь идет в основном о том, какое влияние эта недооценка оказывает на личные финансы – в частности, при капитализации процентов.

Капитализация процентов приносит осторожному держателю сбережений больше денег. Он не просто получает процент с изначально инвестированной суммы, но и добавляет на счет процент, заработанный, скажем, за год. Затем на этот процент тоже начисляются проценты. Если вы положите 100 фунтов под 10 % годовых, то по истечении первого года у вас будет 110 фунтов. Но по истечении второго года вы заработаете 10 % от 110 фунтов, то есть 11 фунтов. По истечении следующего года вам выплатят 10 % от 121 фунта. При капитализации процентов доходность по инвестициям растет экспоненциально.

К несчастью, точно так же дело обстоит со ссудами. Если задолженность по ссуде будет расти экспоненциально из-за неисполнения обязательств по кредиту и начисления процентов, в вашем бюджете могут возникнуть немалые бреши[135]. Мало того, что мы недооцениваем скорость экспоненциального роста, мы еще и переоцениваем свою способность работать с числами. Иными словами, мы понимаем экспоненты неправильно, но при этом проявляем опасную самоуверенность, то есть обычно не проверяем свои интуитивные выводы и не обращаемся за помощью к профессионалам[136].

В применении к эпидемиям недооценка экспоненциального роста дает нам подобное ложное чувство безопасности[137]. В начале вспышки вируса число заражений в день обычно растет экспоненциально, как можно видеть на графике распространения COVID-19 в США в марте 2020 года. И все-таки мы смотрим на первые цифры, и мозг твердит нам, что рост линеен.

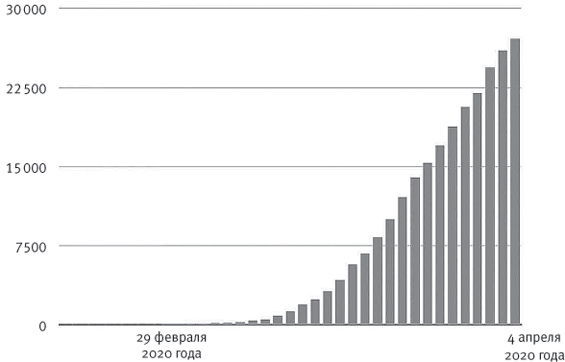
Число случаев заражения COVID-19 в день в начале 2020 года в США (источник: Центр по контролю и профилактике заболеваний)

Пусть в первый день было выявлено 50 случаев, а во второй – 100. Совершая ошибку экспоненциального роста, мы интуитивно предполагаем, что в третий день прибавится еще 50 случаев. Но если рост идет по экспоненциальному закону, дневное увеличение числа случаев с 50 до 100 значит, что каждый день число заболевших удваивается. Следовательно, в третий день заболеет 200 человек, а не 150. К десятому дню будет выявлено на 25 тысяч больше случаев, чем в нашем предполагаемом линейном сценарии. Ошибка приводит к беспечности: мы считаем, что столкнемся с гораздо меньшим числом заболевших, чем на самом деле. Порой наш не склонный к математике мозг оказывается более опасным, чем можно предположить.

Переход к логарифмам

Слово “экспоненциальный” происходит от слова “экспонента”. Экспонентами называются показатели степени – маленькие циферки, стоящие сверху и говорящие, сколько раз нужно умножить число, к которому они относятся, на само себя. Когда мы говорим, что 2³ = 8, на самом деле мы имеем в виду, что нужно “три раза умножить число 2 на само себя”. Это 2 × 2 × 2, то есть 8. Мы также можем перевернуть эти отношения между числами с ног на голову. И здесь в дело вступает логарифм. Вместо того чтобы смотреть на экспоненту, мы можем выразиться иначе и сказать, что “логарифм по основанию 2 от числа 8 равен 3”. Вам может показаться, что толку от этого никакого, но Джон Непер, к счастью, сообразил, что здесь к чему. Он разглядел в этом возможность превратить обременительное умножение в простое сложение.

Математики давно оценили относительную сложность этих операций. Известна чудесная (и, возможно, вымышленная) история немецкого купца XV века, который хотел обучить своего сына математике[138]. Купец обратился за советом к профессору местного университета.

– Если вы хотите, чтобы он просто научился складывать и вычитать, – сказал профессор, – ему достаточно будет окончить немецкий университет.

– А если я хочу, чтобы он научился умножать и делить? – спросил купец.

– Тогда отправьте его в Италию.

Очевидно, немцы тогда еще не освоили умножение. Но Непер показал, что не нужно ехать в Италию, где на папском престоле восседает Антихрист. Он объяснил, как производить умножение путем сложения с помощью тригонометрии.

Помните, как в тригонометрии находят синусы и косинусы? Для этого находится отношение сторон треугольника, вписанного в круг с радиусом 1. Оказывается, эта операция дает любопытный побочный продукт. Возьмем два угла, A и B, и найдем их косинусы. Перемножим их и затем удвоим произведение. Это число окажется равным сумме косинуса угла A + B и косинуса угла A – B. На языке математики:

2cos(A)cos(B) = cos(A + B) + cos(A – B)

Это значит, что произведение двух чисел можно найти в тригонометрических таблицах. Если вы хотите перемножить X и Y, сделайте X равным cos (A), а Y равным cos (B). Откройте буклет с таблицами и найдите A и B. Далее вычислите A + B и A – B. Вернитесь к таблице и найдите косинусы получившихся углов. Сложите их, и получите удвоенное произведение X и Y. Поделите результат пополам – и ответ готов.

Имея набор тригонометрических таблиц, так можно поступать с любыми числами, которые вы хотите перемножить. Непер знал об этой технике и других подобных – например, подобный фокус можно провернуть с помощью синусов углов – и также знал, что моряки и астрономы часто применяли эти “тригонометрические тождества”, чтобы ориентироваться по небу. Но особенно он заинтересовался вопросом, когда узнал от своего знакомого Джона Крейга, что Тихо Браге применил эти техники, чтобы совершить великое открытие[139]. Крейг видел, как Браге с помощниками работает с техникой, когда посетил обсерваторию Браге на острове Вен, где остановился в принадлежащем Браге Ураниборге (буквально – “небесный замок”). Браге использовал тригонометрические тождества в процессе открытия новой звезды, и Непер счел, что дальнейшие открытия можно ускорить, если астрономам будет проще их применять – и особенно если за них уже выполнят всю сложную работу. Он решил, что займется ею сам.

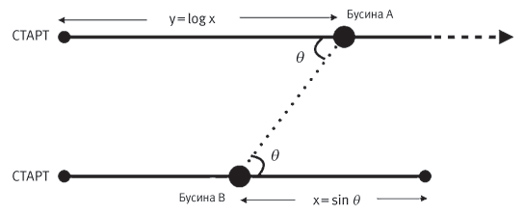
Предложенный Джоном Непером метод вычисления логарифмов