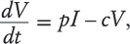
где
В год выхода статьи Перельсона число подтвержденных случаев заражения СПИДом в США достигло внушительных 100 тысяч, и Конгресс создал Национальную комиссию по СПИДу. Модель Перельсона стала спасительной соломинкой для утопающего. Вскоре Перельсон вместе с врачами и исследователями занялся доработкой модели и уточнением ее параметров. Пожалуй, самым значимым стало его партнерство с Дэвидом Хо, в прошлом физиком, а ныне биологом: с помощью математического анализа они доказали, что комбинация трех “антиретровирусных” препаратов, по сути, избавляет организм от ВИЧ[108]. Предлагалась “тройная терапия”: коктейль из трех антиретровирусных препаратов, который превращал ВИЧ из смертного приговора в поддающуюся решению проблему.
Существует множество примеров дифференциальных уравнений, совершенствующих здравоохранение, от анализа циркуляции крови до оценки темпов распространения рака и эффектов химиотерапии. Но дифференциальные уравнения оказали и более заметное влияние на человеческую жизнь. Когда вы идете или едете по подвесному мосту – например, по Бруклинскому мосту в Нью-Йорке или по мосту Акаси-Кайкё через пролив Акаси в Японии, – вы полагаетесь на умение их конструкторов работать с дифференциальными уравнениями. Одной математики для постройки мостов недостаточно, но начинается все именно с расчетов – как правило, с набора дифференциальных уравнений, описывающих взаимодействие массы, прочности и сопротивления движению, характерных для используемых материалов. Например, инженерам порой приходится рассматривать дифференциальное уравнение, которое описывает, как изменение расстояния между несущими тросами влияет на степень их натяжения, и выбирать конфигурацию, которая минимизирует изменение натяжения при увеличении нагрузки на мост (в таком случае крутизна кривой, описывающей отношение натяжения к нагрузке, должна быть близка к нулю), чтобы сделать конструкцию максимально безопасной. Дифференциальные уравнения находят применение и при проектировании небоскребов: с их помощью рассчитывается, как будет меняться нагрузка на фундамент при увеличении высоты здания и как сильно здание будет поворачиваться и колебаться в шторм. Все находящиеся в зоне вашей видимости здания, дороги, тоннели и мосты, построенные менее ста пятидесяти лет назад, проектировались с использованием математического анализа.
Дифференцирование – лишь одна сторона медали математического анализа. На другой стороне находится интегрирование – противоположность дифференцированию (хотя, когда его изобрели, об этом никто еще не догадывался). Интегрирование предполагает сложение площадей под крошечными отрезками кривой. Зачем это вообще нужно? Дело в том, что часто это позволяет понять, как ведет себя некая система – будь то экономика страны, спутник на орбите или тропический шторм.
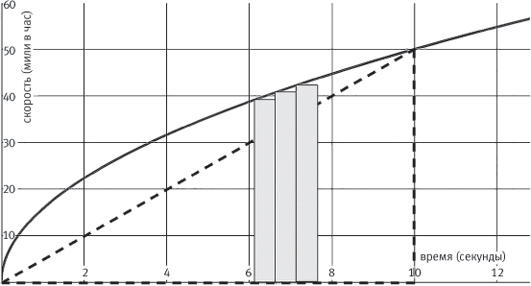
Методы вычисления площади под кривой
Классический пример обычно проще. Допустим, ваш автомобиль разгоняется из неподвижного состояния. Через 5 секунд он едет со скоростью 36 миль в час, а через 10 секунд достигает скорости 50 миль в час. Если построить график изменения его скорости во времени, он будет примерно таким, как на рисунке.
Теперь допустим, что вы хотите выяснить кое-что новое: как далеко продвинулся автомобиль за 10 секунд. У вас есть только данные о скорости и времени. Но подумайте: скорость измеряется в милях в час, а время – в часах (которые при необходимости можно разделить на секунды). Если перемножить скорость и время, получим:
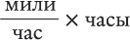
Ответом будут одни мили, то есть расстояние. Иными словами, при перемножении вертикальной и горизонтальной величин, как и при вычислении площади квадрата или прямоугольника, мы получаем новые данные. Единственная проблема в том, что график – это не квадрат и не прямоугольник, поэтому вычислить его площадь не так просто. Можно получить примерный результат с помощью прямоугольного треугольника, обозначенного на рисунке пунктиром, но многое тогда останется неучтенным. Лучше разделить область под кривой на ряд прямоугольников (как три серых на рисунке) и сложить их площади вместе. Но даже такое вычисление будет не слишком точным – если только не построить множество прямоугольников ничтожно малой ширины. Под множеством я имею в виду бесконечное множество. А под ничтожно малой шириной – бесконечно малую.
Рассмотрим ситуацию, в которой зависимость
Поделив обе части уравнения на
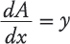
Помните, как мы вычисляли
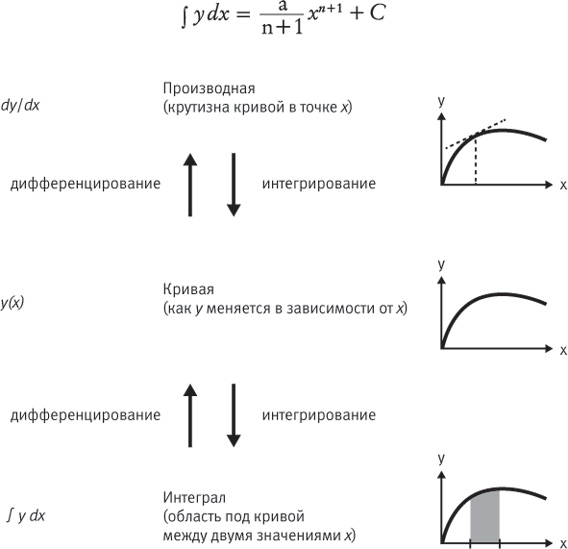
Отношения между кривыми и их производными и интегралами
Как и дифференцирование, интегрирование используется во множестве сфер современной жизни. Например, при прогнозировании погоды и моделировании климата необходимо интегрировать количество солнечного света, поступающего на поверхность Земли. Интегрирование прогнозируемого количества осадков позволяет установить, существует ли опасность наводнения. Инженеры NASA применяют интегралы, чтобы прокладывать траектории полетов: когда одна из первых темнокожих женщин-математиков Кэтрин Джонсон рассчитывала сначала орбиту миссии Алана Шепарда “Фридом-7”, состоявшейся в 1961 году, а год спустя – орбиту миссии Джона Гленна “Френдшип-7”, она не могла не прибегать к интегрированию. К счастью, она была в нем профи – и ее авторитет был настолько велик, что Гленн даже попросил, чтобы отныне только она проверяла данные с нового электронного компьютера[109].
Сегодня интегрирование – довольно простая операция, которая входит в стандартный инструментарий математика. Тем не менее открыть его оказалось чрезвычайно сложно. Лейбниц и Ньютон пришли к нему с разных сторон. Ньютон так далеко продвинулся в сфере дифференцирования, что даже не пытался объяснить свои приемы современникам. Однажды он довольно высокомерно заявил, что “меньше чем за четверть часа” может вычислить площадь области под любой кривой. Столь головокружительная скорость, добавил он, достигается благодаря “источнику, который [его] питает, но ничего доказывать [он] при этом не [собирается]”[110]. Он рассчитывал, что знание графиков и геометрии поможет его современникам изучить основы этой операции.
Несомненно, многие из них тогда почувствовали себя идиотами. Математический анализ часто обескураживает людей при первой встрече с ним. Хотя мы в состоянии следовать алгоритму и получать верные ответы, идеи, лежащие в основе математического анализа, его производные и требуемый полет фантазии поистине поражают своей сложностью. Архимед сделал первые шаги к решению схожих задач более чем за тысячу лет до того, как Ньютон и Лейбниц предложили свои решения. Такие светила математики, как Декарт и Ферма, сумели разглядеть лишь тень анализа. Чтобы по-настоящему погрузиться в него, нужно представлять себе бесконечное и бесконечно малое. Нужно понимать (а Ферма и Декарт не понимали), что касательная к кривой (прямая, которая касается ее в одной точке) показывает крутизну кривой в точке соприкосновения и позволяет узнать все характеристики этой кривой. Нужно уметь выстраивать длинные цепочки сумм, называемые бесконечными рядами, как умели это и Ньютон, и Лейбниц, а также замечать параметры, исключающие друг друга и открывающие скрытый путь сквозь густой подлесок ваших производных. Неслучайно математический анализ развивался целое тысячелетие.
Сейчас вы, возможно, задаетесь вопросом, кто вообще мог такое придумать. Как правило, это люди, с которыми вам, пожалуй, не захотелось бы водить компанию. Например, Пьер Ферма, который днем работал судьей и адвокатом в судах Тулузы, вечера проводил в уединении от семьи за решением математических задач. Он при этом не стремился поделиться своими открытиями с миром и не опубликовал ни одного из своих выводов. Мы знаем о них лишь потому, что их обнаружили в его записных книжках и дневниках уже после его смерти.
Впрочем, Ферма писал о некоторых своих открытиях другим математикам. Так о нем и услышал Рене Декарт, которому рассказал о нем их общий знакомый Марен Мерсенн. Декарт, в отличие от Ферма, был не лишен самодовольства. Один современник назвал его “холодным и себялюбивым”. Хвастаясь, что нашел способ строить касательные к любой кривой, Декарт сказал: “Эта задача является наиболее полезной не только среди известных мне, но также среди всех тех задач, которые я когда-либо желал знать в геометрии”[111].
Декарт ужасно огорчился, узнав от Мерсенна, что Ферма решил эту задачу на десять лет раньше. Чтобы выставить себя в лучшем свете, Декарт изучил доказательства Ферма и во всеуслышание заявил, что нашел в них целый ряд досадных ошибок, хотя на самом деле ошибок в них не было.